题目内容
2.在△ABC中,角A,B,C的对边分别为a,b,c,向量$\overrightarrow m}$=(4b,$\sqrt{7}$),$\overrightarrow n}$=(a,sinA)满足$\overrightarrow m}$∥$\overrightarrow n}$.(Ⅰ)求sinB的值;
(Ⅱ)若a,b,c成等差数列,且公差大于0,求cosA-cosC的值.
分析 (Ⅰ)通过$\overrightarrow m∥\overrightarrow n$可得4bsinA=$\sqrt{7}$a,利用正弦定理计算即得结论;
(Ⅱ)通过a、b、c成等差数列可得a+c=2b,利用正弦定理及平方关系计算即可.
解答 解:(Ⅰ)∵$\overrightarrow m=(4b,\sqrt{7}),\overrightarrow n=(a,sinA)$,$\overrightarrow m∥\overrightarrow n$,
∴4bsinA=$\sqrt{7}$a,
根据正弦定理得4sinBsinA=$\sqrt{7}$sinA,
∴sinB=$\frac{\sqrt{7}}{4}$;
(Ⅱ)∵a、b、c成等差数列,∴a+c=2b,
由正弦定理以及(Ⅰ)得sinA+sinC=$\frac{\sqrt{7}}{2}$ ①
设cosA-cosC=x ②
①2+②2,得2-2cos(A+C)=$\frac{7}{4}$+x2 ③
又a<b<c,A<B<C,∴0°<B<90°,cosA>cosC,
故cos(A+C)=-cosB=-$\frac{3}{4}$.
代入③式得x2=$\frac{7}{4}$,
∴cosA-cosC=$\frac{\sqrt{7}}{2}$.
点评 本题考查向量数量积的运算、等差数列、正弦定理等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.已知圆x2+y2+x+2y=$\frac{61}{16}$和圆(x-sinα)2+(y-1)2=$\frac{1}{16}$,其中0°≤α≤90°,则两圆的位置关系是( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 相交或内切 |
13.已知集合M={x|y=lg(1-x)},集合N={y|y=2x,x∈R},则M∩N=( )
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
17.已知全集U=R,集合A={y|y=2x,x∈R},B={x|x≥2},则下图中阴影部分所表示的集合为( )
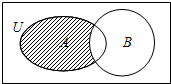

| A. | ∅ | B. | {0,1} | C. | (0,2) | D. | (-∞,2) |
 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.