题目内容
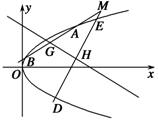
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足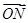 =
=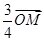 ,O为坐标原点.
,O为坐标原点.
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
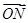 =
=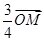 ,O为坐标原点.
,O为坐标原点.
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
(1)y2=4x(2)(10,0)
∵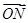 =
=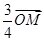 ,点M的坐标为(12,8),可得点N的坐标为(9,6),∴62=18p,∴p=2,所以抛物线C的方程为y2=4x.
,点M的坐标为(12,8),可得点N的坐标为(9,6),∴62=18p,∴p=2,所以抛物线C的方程为y2=4x.
(2)证明:由条件可知,直线l1,l2的斜率存在且不为0,设l1:y=k(x-12)+8,则l2的方程为y=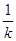 (x-12)+8,由
(x-12)+8,由 得ky2-4y+32-48k=0,设A(x1,y1),B(x2,y2),则y1+y2=
得ky2-4y+32-48k=0,设A(x1,y1),B(x2,y2),则y1+y2= ,又y1+y2=k(x1+x2-24)+16,∴x1+x2=
,又y1+y2=k(x1+x2-24)+16,∴x1+x2= -
- +24,∴点G的坐标为
+24,∴点G的坐标为 ,用
,用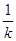 代替k,得到点H坐标为(2k2-8k+12,2k),∴kGH=
代替k,得到点H坐标为(2k2-8k+12,2k),∴kGH=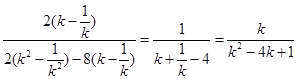
∴lGH:y-2k= [x-(2k2-8k+12)].
[x-(2k2-8k+12)].
令y=0,则x=10,所以直线GH过定点(10,0)
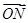 =
=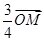 ,点M的坐标为(12,8),可得点N的坐标为(9,6),∴62=18p,∴p=2,所以抛物线C的方程为y2=4x.
,点M的坐标为(12,8),可得点N的坐标为(9,6),∴62=18p,∴p=2,所以抛物线C的方程为y2=4x.(2)证明:由条件可知,直线l1,l2的斜率存在且不为0,设l1:y=k(x-12)+8,则l2的方程为y=
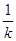 (x-12)+8,由
(x-12)+8,由 得ky2-4y+32-48k=0,设A(x1,y1),B(x2,y2),则y1+y2=
得ky2-4y+32-48k=0,设A(x1,y1),B(x2,y2),则y1+y2= ,又y1+y2=k(x1+x2-24)+16,∴x1+x2=
,又y1+y2=k(x1+x2-24)+16,∴x1+x2= -
- +24,∴点G的坐标为
+24,∴点G的坐标为 ,用
,用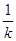 代替k,得到点H坐标为(2k2-8k+12,2k),∴kGH=
代替k,得到点H坐标为(2k2-8k+12,2k),∴kGH=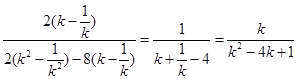
∴lGH:y-2k=
 [x-(2k2-8k+12)].
[x-(2k2-8k+12)].令y=0,则x=10,所以直线GH过定点(10,0)

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
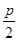 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.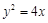 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .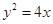 的焦点为
的焦点为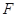 ,点
,点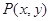 为该抛物线上的动点,又点
为该抛物线上的动点,又点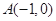 ,则
,则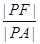 的最小值是( )
的最小值是( ) 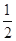
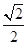

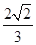
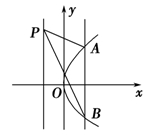
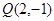 ,F为抛物线
,F为抛物线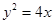 的焦点,动点
的焦点,动点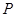 为抛物线上任意一点,当
为抛物线上任意一点,当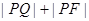 取最小值时P的坐标为________.
取最小值时P的坐标为________.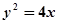 与双曲线
与双曲线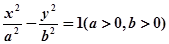 有相同的焦点F,点
有相同的焦点F,点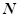 是两曲线的交点,且
是两曲线的交点,且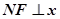 轴,则
轴,则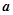 的值为( )
的值为( )