Question

【题目】已知函数y=f（x）是定义在R上的偶函数，对于x∈R，都有f（x+4）=f（x）+f（2）成立，当x1 ， x2∈[0，2]且x1≠x2时，都有 ＜0，给出下列四个命题：
①f（﹣2）=0；
②直线x=﹣4是函数y=f（x）的图象的一条对称轴；
③函数y=f（x）在[4，6]上为增函数；
④函数y=f（x）在（﹣8，6]上有四个零点．
其中所有正确命题的序号为 ．

Answer 1

【答案】①②④
【解析】解：①：对于任意x∈R，都有f（x+4）=f （x）+f （2）成立，令x=﹣2，则f（﹣2+4）=f（﹣2）+f （2）=f（2），
即f（﹣2）=0，即①正确；
②：由（1）知f（x+4）=f （x），则f（x）的周期为4，
又∵f（x）是R上的偶函数，∴f（x+4）=f（﹣x），
而f（x）的周期为4，则f（x+4）=f（﹣4+x），f（﹣x）=f（﹣x﹣4），
∴f（﹣4﹣x）=f（﹣4+x），
则直线x=﹣4是函数y=f（x）的图象的一条对称轴，即②正确；
③：当x1 ， x2∈[0，2]，且x1≠x2时，都有 ＜0，
∴函数y=f（x）在[0，2]上为减函数，
而f（x）的周期为4，
∴函数y=f（x）在[4，6]上为减函数，故③错误；
④：∵f（2）=0，f（x）的周期为4，函数y=f（x）在[0，2]上为增函数，
在[﹣2，0]上为减函数，
∴作出函数在（﹣8，6]上的图象如图：
则函数y=f（x）在（﹣8，6]上有4个零点，故④正确．
所以答案是．①②④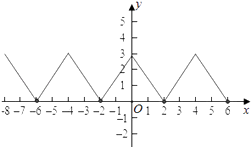

【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识，掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．