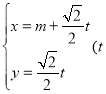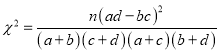题目内容
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率
,离心率![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据题意列出待定系数的方程组,即可求得方程;(2)设![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
易得![]() 的周长为
的周长为![]() ,所以
,所以![]() ,因此
,因此![]() 最大,
最大,![]() 就最大. 把
就最大. 把![]() 分解为
分解为![]() 和
和![]() ,从而得到
,从而得到![]() ,整理方程组, 求出两根和与两根既即得到面积
,整理方程组, 求出两根和与两根既即得到面积![]() 与
与![]() 的函数关系,通过换元,利用均值不等式即可求得
的函数关系,通过换元,利用均值不等式即可求得![]() 的最大值
的最大值![]() ,此时
,此时![]() .
.
试题解析:(1)由题意可得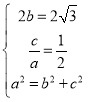 ...................2分
...................2分
解得![]() ..................3分
..................3分
故椭圆的标准方程为![]() ..................... 4分
..................... 4分
(2)设![]() ,设
,设![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
因为![]() 的周长为
的周长为![]() ,
,![]() ,
,
因此![]() 最大,
最大,![]() 就最大........................6分
就最大........................6分
![]() ,
,
由题意知,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,
,
由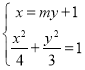 得
得![]() ,
,
所以,![]() .................8分
.................8分
又因直线![]() 与椭圆
与椭圆![]() 交于不同的两点,
交于不同的两点,
故![]() ,即
,即![]() ,则
,则
![]() ............10分
............10分
令![]() ,则
,则![]() ,
,
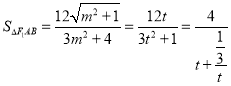 .
.
令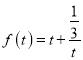 ,由函数的性质可知,函数
,由函数的性质可知,函数![]() 在
在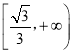 上是单调递增函数,
上是单调递增函数,
即当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
因此有![]() ,所以
,所以![]() ,
,
即当![]() 时,
时,![]() 最大,此时
最大,此时![]() ,
,
故当直线![]() 的方程为
的方程为![]() 时,
时,![]() 内切圆半径的最大值为
内切圆半径的最大值为![]() ...........12分
...........12分

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(2)针对于问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中男生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: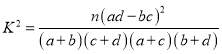 ,其中
,其中![]() )
)