题目内容
6.如图1,圆O的半径为2,AB,CE均为该圆的直径,弦CD垂直平分半径OA,垂足为F,沿直径AB将半圆ACB所在平面折起,使两个半圆所在的平面互相垂直(如图2)(Ⅰ)求四棱锥C-FDEO的体积
(Ⅱ)如图2,在劣弧BC上是否存在一点P(异于B,C两点),使得PE∥平面CDO?若存在,请加以证明;若不存在,请说明理由.

分析 (Ⅰ)在图1中由平面几何知识求出梯形FDEO的面积,再由图2证得CF⊥平面ADE,并求出FE,然后代入棱锥的体积公式得答案;
(Ⅱ)取劣弧BC的中点,利用三角形中的边角关系证得四边形CDEP为平行四边形,再由线面平行的判定得答案.
解答 解:(Ⅰ)如图1,∵弦CD垂直平分半径OA,半径为2,
∴CF=DF,OF=$\frac{1}{2}OC=1$,
∴在Rt△COF中有∠COF=60°,CF=DF=$\sqrt{3}$,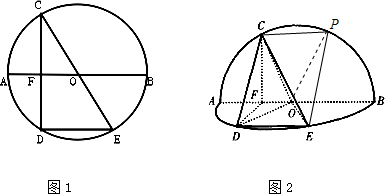 ∵CE为直径,∴DE⊥CD,
∵CE为直径,∴DE⊥CD,
∴OF∥DE,DE=2OF=2,
∴${S}_{梯形FDEO}=\frac{1}{2}(OF+DE)•DF=\frac{3}{2}\sqrt{3}$,
图2中,平面ACB⊥平面ADE,平面ACB∩平面ADE=AB,
又CF⊥AB,CF?平面ACB,
∴CF⊥平面ADE,则CF是四棱锥C-FDEO的高,
∴${V}_{C-FDEO}=\frac{1}{3}{S}_{梯形FDEO}•CF=\frac{3}{2}$.
(Ⅱ)在劣弧BC上是存在一点P(劣弧BC的中点),使得PE∥平面CDO.
证明:分别连接PE,CP,OP,
∵点P为劣弧BC弧的中点,∴$∠COP=\frac{1}{2}∠COB$,
∵∠COF=60°,∴∠COP=60°,则△COP为等边三角形,
∴CP∥AB,且$CP=\frac{1}{2}AB$,又∵DE∥AB且DE=$\frac{1}{2}AB$,
∴CP∥DE且CP=DE,
∴四边形CDEP为平行四边形,
∴PE∥CD,
又PE?面CDO,CD?面CDO,
∴PE∥平面CDO.
点评 本题以空间几何体的翻折为背景,考查空间几何体的体积,考查空间点、线、面的位置关系、线面平行及线面垂直等基础知识,考查空间想象能力,求解运算能力和推理论证能力,考查数形结合,化归与数学转化等思想方法,是中档题.

| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | a<c<b |
| A. | $-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | B. | $\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$ | C. | $-\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | D. | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ |
| 类别 | A | B | C |
| 数量 | 4 | 3 | 2 |
(Ⅰ)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(Ⅱ)若一次性提取4辆车,其中A,B,C三种型号的车辆数分别记为a,b,c,记ξ为a,b,c的最大值,求ξ的分布列和数学期望.
 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=2.