题目内容
(本小题满分12分)
已知甲、乙两个工厂在今年的1月份的利润都是6万,且乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2—4x+6,g(x)=a2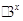 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).
(1)求函数f(x)与g(x)的解析式;
(2)求甲、乙两个工厂今年5月份的利润;
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图,并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况.
(1) f(x)=4x2-4x+6. g(x)=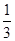 ×3x+5=3x-1+5.(2)甲、乙两个工厂今年5月份的利润相等.(3)作函数图像如下:
×3x+5=3x-1+5.(2)甲、乙两个工厂今年5月份的利润相等.(3)作函数图像如下: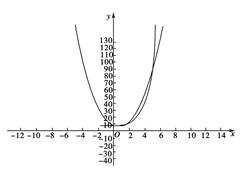
当x=1或x=5时,有f(x)=g(x); 当1<x<5时,有f(x)>g(x); 当5<x≤10时,有f(x)<g(x).
解析试题分析:(1)依题意:由f(1)=6,解得:a1=4, ∴f(x)=4x2-4x+6.
由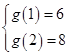 ,有
,有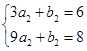 ,
,
解得a2=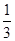 ,b2=5, ∴g(x)=
,b2=5, ∴g(x)=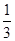 ×3x+5=3x-1+5.
×3x+5=3x-1+5.
(2)由(1)知甲厂在今年5月份的利润为f(5)=86万元,乙厂在今年5月份的利润为g(5)=86万元,故有f(5)=g(5),即甲、乙两个工厂今年5月份的利润相等.
(3)作函数图像如下: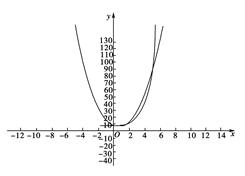
从图中可以看出今年1—10月份甲、乙两个工厂的利润:
当x=1或x=5时,有f(x)=g(x); 当1<x<5时,有f(x)>g(x); 当5<x≤10时,有f(x)<g(x).
考点:本题考查了函数解析式及图象的实际运用
点评:与函数有关的应用题,经常涉及物价、路程、产值、环保等实际问题,也可涉及角度、面积、体积、造价的最优化问题,解答这类问题的关键是确切建立相关函数解析式,然后应用函数、方程和不等式的有关知识加以综合解答

 (2)
(2)
 ,设
,设
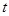 的取值范围,使得函数
的取值范围,使得函数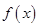 在
在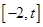 上为单调函数;
上为单调函数; 满足
满足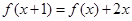 且
且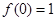 .
.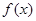 的解析式;
的解析式; 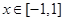 时,不等式:
时,不等式: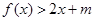 恒成立,求实数
恒成立,求实数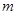 的范围.
的范围.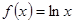 ,
,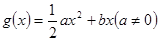
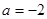 时,
时,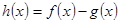 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围; 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 ,
,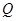 两点,过线段
两点,过线段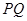 的中点
的中点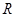 作
作 轴的垂线分别交
轴的垂线分别交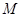 ,
, ,问是否存在点
,问是否存在点
 ,其中
,其中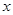 是仪器的月产量
是仪器的月产量 表示为月产量
表示为月产量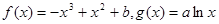 ,
, 在
在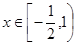 上的最大值为
上的最大值为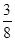 ,求实数
,求实数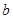 的值;
的值;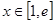 ,都有
,都有 恒成立,求实数
恒成立,求实数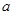 的取值范围;
的取值范围;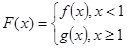 ,对任意给定的正实数
,对任意给定的正实数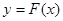 上是否存在两点
上是否存在两点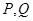 ,使得
,使得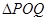 是以
是以 (
( 轴上?请说明理由。
轴上?请说明理由。