题目内容
(本题满分12分)
已知二次函数 满足
满足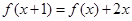 且
且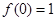 .
.
(Ⅰ)求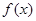 的解析式;
的解析式;
(Ⅱ)当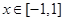 时,不等式:
时,不等式: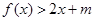 恒成立,求实数
恒成立,求实数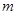 的范围.
的范围.
(Ⅰ)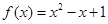 ;(Ⅱ)
;(Ⅱ)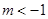
解析试题分析:(Ⅰ)令 代入:
代入:
得: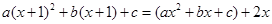
即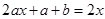 对于任意的
对于任意的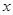 成立,则有
成立,则有
∴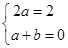 解得
解得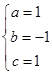 ∴
∴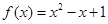 6分
6分
(Ⅱ)当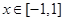 时,
时,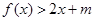 恒成立
恒成立
即: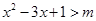 恒成立; 8分
恒成立; 8分
令 ,
,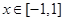
∵开口方向向上,对称轴: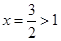 ,∴
,∴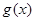 在
在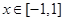 内单调递减;
内单调递减;
∴ ∴
∴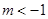 12分
12分
考点:本题考查了函数解析式的求法及恒成立问题
点评:二次函数在指定区间上的恒成立问题,可以利用韦达定理以及根的分布知识求解,属基础题

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,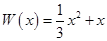 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,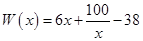 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完. (万元)关于年产量
(万元)关于年产量 固定成本
固定成本 (单位:元/千克)满足关系式y=
(单位:元/千克)满足关系式y=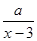 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克. (单位:元,
(单位:元, )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.(I)将一个星期的商品销售利润表示成 (a为常数),
(a为常数),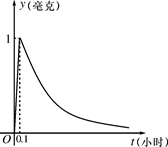
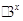 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R). (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?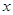 天(
天(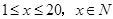 )的销售价格(单位:元)为
)的销售价格(单位:元)为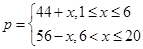 ,第
,第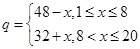 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.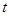 关于第
关于第