题目内容
2.小华准备购买一台售价为5000元的电脑,采用分期付款方式,并在一年内将款全部付清,商场提出的付款方式为:购买后二个月第一次付款,再过二个月第二次付款…,购买后12个月第六次付款,每次付
款金额相同,约定月利率为0.8%每月利息按复利计算.求小华每期付款的金额是多少?
分析 通过从小华每次还款后还欠商场的金额这个角度出发,利用最后一次还款为0,计算即得结论.
解答 解:设小华每期还款x元、第k个月末还款后的本利欠款数为Ak元,
则:A2=5000•(1+0.008)2-x,
A4=A2•(1+0.008)2-x
=5000•(1+0.008)4-(1+0.008)2x-x,
…
A12=A10•(1+0.008)12-x
=5000•(1+0.008)12-(1+0.008)10x-…-(1+0.008)4x-(1+0.008)2x-x,
由题意年底还清,即A12=0,
解得:x=$\frac{5000•1.00{8}^{12}}{1+1.00{8}^{2}+1.00{8}^{4}+…+1.00{8}^{10}}$
≈880.8(元),
答:小华每期还款的金额为880.8元.
点评 本题考查函数模型的选择与应用,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.
注:本题还可以从“各期所付的款额连同最后一次付款时所生的利息之和等于商品售价及从购买到最后一次付款时的利息之和”这个角度来解题.

练习册系列答案
相关题目
13.某几何体的三视图如下图所示,则该几何体为( )
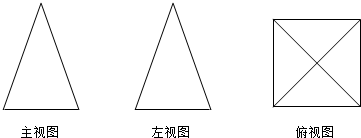

| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 四棱锥 |
17.在△ABC中,sinC=$\frac{sinA+sinB}{cosA+cosB}$,则△ABC一定是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
7.直线a∥α,直线b⊥α,那么直线a与直线b的位置关系一定是( )
| A. | 平行 | B. | 异面 | C. | 垂直 | D. | 不相交 |
1.已知方程ex-x+a=0(a为常数)有两个不等实根,则实数a的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,-1] |
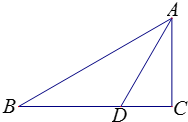 已知△ABC中,AD是∠BAC的角平分线,交BC于D,BD=2DC.
已知△ABC中,AD是∠BAC的角平分线,交BC于D,BD=2DC.