题目内容
12．在某电视歌曲大奖赛中，最有六位选手争夺一个特别奖，观众A，B，C，D猜测如下：A说：获奖的不是1号就是2号；A说：获奖的不可能是3号；C说：4号、5号、6号都不可能获奖；D说：获奖的是4号、5号、6号中的一个．比赛结果表明，四个人中恰好有一个人猜对，则猜对者一定是观众C获特别奖的是3号选手．分析 由4人中只有1人猜对，结合C与D互相否定，可知猜对者是C、D中的一人．然后假定D对，可得B也对，与题设矛盾，结合B一定猜错，可知获奖者是3号选手．
解答 解：推理如下：因为只有一人猜对，而C与D互相否定，故C、D中一人猜对．
假设D对，则推出B也对，与题设矛盾，故D猜错，所以猜对者一定是C；
于是B一定猜错，故获奖者是3号选手（此时A错）．
故答案为：C；3．
点评 本题考查简单的合情推理，题目的难点主要出现在读题上，需要仔细分析，属中档题．
练习册系列答案
相关题目
3．已知n∈N*，且n＞1，三个数ln$\frac{n+1}{n}$、$\frac{1}{n+1}$、$\frac{1}{n}$的大小关系是（ ）
| A． | $\frac{1}{n}$＞ln$\frac{n+1}{n}$＞$\frac{1}{n+1}$ | B． | ln$\frac{n+1}{n}$＞$\frac{1}{n}$＞$\frac{1}{n+1}$ | C． | $\frac{1}{n}$＞$\frac{1}{n+1}$＞ln$\frac{n+1}{n}$ | D． | $\frac{1}{n+1}$＞$\frac{1}{n}$＞ln$\frac{n+1}{n}$ |
7．老张身高176cm，他爷爷、父亲、儿子的身高分别是173cm、170cm和182cm，因儿子的身高与父亲的身高有关，用回归分析的方法得到的回归方程为$\widehat{y}$=x+$\widehat{a}$，则预计老张的孙子的身高为（ ）cm．
| A． | 182 | B． | 183 | C． | 184 | D． | 185 |
17．2015年6月20日是我们的传统节日--”端午节”，这天小明的妈妈为小明煮了5个粽子，其中两个腊肉馅三个豆沙馅，小明随机取出两个，事件A=“取到的两个为同一种馅”，事件B=“取到的两个都是豆沙馅”，则P（B|A）=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{10}$ | D． | $\frac{3}{10}$ |
4．△ABC中，角A、B、C所对应的边分别a、b、c，已知bcosC+ccosB=2b，则$\frac{a}{2b}$=（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | $\sqrt{2}$ | D． | 1 |
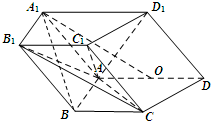如图，在四棱柱ABCD-A1B1C1D1中，侧面ADD1A1⊥底面ABCD，D1A=D1D=$\sqrt{2}$，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点．