题目内容
11.在△ABC中,角A,B,C所对的边分别为a,b,c,且sin2C+$\sqrt{3}$cos(A+B)=0(1)若a=4,c=$\sqrt{13}$,求△ABC的面积;
(2)若A=$\frac{π}{3}$,cosB>cosC,求$\overrightarrow{AB}•\overrightarrow{BC}-2\overrightarrow{BC}•\overrightarrow{CA}-3\overrightarrow{CA}•\overrightarrow{AB}$的值.
分析 (1)先化简条件求出C的大小,结合三角形的面积公式即可求出△ABC的面积;
(2)由A=$\frac{π}{3}$,cosB>cosC,求出C的大小,结合向量的数量积公式进行化简即可求$\overrightarrow{AB}•\overrightarrow{BC}-2\overrightarrow{BC}•\overrightarrow{CA}-3\overrightarrow{CA}•\overrightarrow{AB}$的值.
解答 解:(1)∵sin2C+$\sqrt{3}$cos(A+B)=0
∴2sinCcosC-$\sqrt{3}$cosC=0,
即cosC(2sinC-$\sqrt{3}$)=0,
即cosC=0,或sinC=$\frac{\sqrt{3}}{2}$
即C=$\frac{π}{2}$或C=$\frac{π}{3}$或C=$\frac{2π}{3}$,
∵a=4,c=$\sqrt{13}$,
∴a>c,
即C不是最大值,
则C=$\frac{π}{3}$,
则c2=b2+a2-2abcos$\frac{π}{3}$,
即13=16+b2-2b×$4×\frac{1}{2}$,
即b2-4b+3=0,
解得b=1或b=3,
若b=1,则三角形的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}×4×1×\frac{\sqrt{3}}{2}$=$\sqrt{3}$
若b=3,则三角形的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}×4×3×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$;
(2)由(1)知C=$\frac{π}{2}$或C=$\frac{π}{3}$或C=$\frac{2π}{3}$,
若A=$\frac{π}{3}$,
则C=$\frac{2π}{3}$不成立,舍去,
∵cosB>cosC,
∴B<C,
则C>$\frac{π}{3}$,
∴C=$\frac{π}{2}$,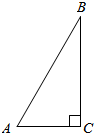
即三角形为直角三角形.
则b=$\frac{1}{2}$c,a=$\frac{\sqrt{3}}{2}$c,
则$\overrightarrow{AB}•\overrightarrow{BC}-2\overrightarrow{BC}•\overrightarrow{CA}-3\overrightarrow{CA}•\overrightarrow{AB}$=accos150°-0-3bccos120°=$-\frac{\sqrt{3}}{2}$ac+$\frac{3}{2}$bc=-$\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}$c2+$\frac{3}{2}$×$\frac{1}{2}$c2=$-\frac{3}{4}$c2+$\frac{3}{4}$c2=0
点评 本题主要考查向量数量积的应用,根据条件求出C的大小是解决本题的关键.考查学生的计算能力.

| 日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(2)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.)
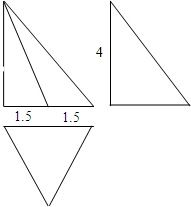 如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )
如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )| A. | 19π | B. | 28π | C. | 67π | D. | 76π |
| A. | 210 | B. | -210 | C. | -910 | D. | 280 |
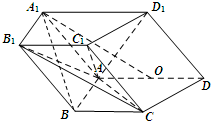 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.