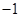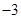题目内容
下列区间中，函数f（x）=|ln（2-x）|在其上为增函数的是（ ）
| A．（-∞，1] | B．[-1，
| C．[0，
| D．[1，2） |
由2-x＞0得，x＜2，∴f（x）的定义域为（-∞，2），
当x＜1时，ln（2-x）＞0，f（x）=|ln（2-x）|=ln（2-x），
∵y=lnt递增，t=2-x递减，∴f（x）单调递减；
当1≤x＜2时，ln（2-x）≤0，f（x）=|ln（2-x）|=-ln（2-x），
∵y=-t递减，t=ln（2-x）递减，
∴f（x）递增，即f（x）在[1，2）上单调递增，
故选D．
当x＜1时，ln（2-x）＞0，f（x）=|ln（2-x）|=ln（2-x），
∵y=lnt递增，t=2-x递减，∴f（x）单调递减；
当1≤x＜2时，ln（2-x）≤0，f（x）=|ln（2-x）|=-ln（2-x），
∵y=-t递减，t=ln（2-x）递减，
∴f（x）递增，即f（x）在[1，2）上单调递增，
故选D．
练习册系列答案
名师点拨卷系列答案
相关题目
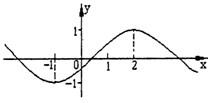
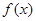是周期为4的奇函数，当
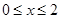时，
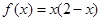，则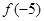
等于 （ ）
