题目内容
11.利用函数的单调性比较下列各组中两个三角函数值的大小;(1)sin103°15′与sin164°30′;
(2)cos(-$\frac{47}{10}$π)与cos(-$\frac{44}{9}$π);
(3)sin508°与sin144°;
(4)cos760°与cos(-770°)
分析 根据三角函数的单调性进行判断即可.
解答 解:(1)y=sinx在(90°,180°)上为减函数,
∴sin103°15′>sin164°30′;
(2)cos(-$\frac{47}{10}$π)=cos(-4π-$\frac{7π}{10}$)=cos(-$\frac{7π}{10}$)=cos$\frac{7π}{10}$,
cos(-$\frac{44}{9}$π)=cos(-4π-$\frac{8π}{9}$)=)=cos(-$\frac{8π}{9}$)=cos$\frac{8π}{9}$,
∵y=cosx在(0,π)上为减函数,
∴cos$\frac{7π}{10}$>cos$\frac{8π}{9}$,
即cos(-$\frac{47}{10}$π)>cos(-$\frac{44}{9}$π);
(3)sin508°=sin(360°+248°)=sin248°<0,sin144°>0,
则sin508°<sin144°;
(4)cos760°=cos(720°+40°)=cos40°,
cos(-770°)=cos770°=cos(720°+50°)=cos50°,
则cos40°>cos50°,
即cos760°>cos(-770°).
点评 本题主要考查函数的大小比较,根据三角函数的诱导公式以及三角函数的单调性是解决本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
2.设集合A={x|0≤x≤4},B={y|y=-x2,-1≤x≤2},则∁R(A∩B)=( )
| A. | R | B. | {x|x∈R,x≠0} | C. | {0} | D. | ∅ |
19.命题“对任意的x∈R,x3-1≤0”的否定是( )
| A. | 不存在x∈R,x3-1≤0 | B. | 存在x∈R,x3-1≤0 | ||
| C. | 存在x∈R.x3-1>0 | D. | 对任意的x∈R,x3-1>0 |
6.若数列{an}的前n项的和Sn=3an-2,则这个数列的通项公式为( )
| A. | ${a_n}={(\frac{3}{2})^{n-1}}$ | B. | ${a_n}=3×{(\frac{1}{2})^{n-1}}$ | C. | an=3n-2 | D. | ${a_n}={3^{n-1}}$ |
16.已知函数y=$\left\{\begin{array}{l}{{x}^{2}+1(x≤0)}\\{-2x(x>0)}\end{array}\right.$则使函数值为10的x值是( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
20.己知程序框图如图所示,执行相应程序,若输出S=15,则框图中①处可以填入( )
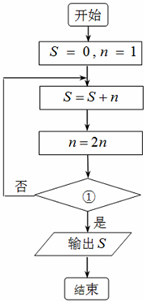

| A. | n≥4? | B. | n>8? | C. | n>4? | D. | n≥8? |
