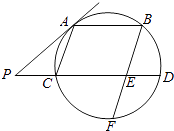题目内容
【题目】已知椭圆 
的长轴长是短轴长的两倍，且过点C（2，1），点C关于原点O的对称点为点D．
（1）求椭圆E的方程；
（2）点P在椭圆E上，直线CP和DP的斜率都存在且不为0，试问直线CP和DP的斜率之积是否为定值？若是，求此定值；若不是，请说明理由：
（3）平行于CD的直线l交椭圆E于M，N两点，求△CMN面积的最大值，并求此时直线l的方程．
【答案】
（1）解：∵2a=22b，∴a=2b．
设椭圆方程为 
．
椭圆E过点C（2，1），
代入椭圆方程得 
，解得 
，则 
，
所以所求椭圆E的方程为 
；
（2）解：依题意得D（﹣2，﹣1）在椭圆E上．
CP和DP的斜率KCP和KDP均存在．
设P（x，y），则 
， 
，
①
又∵点P在椭圆E上，
∴ ，∴x2=8﹣4y2，代入①得，
．
所以CP和DP的斜率KCP和KDP之积为定值 
（3）解：CD的斜率为 
，∵CD平行于直线l，∴设直线l的方程为 
．
由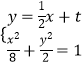 
，
消去y，整理得x2+2tx+（2t2﹣4）=0．
设M（x1，y1），N（x2，y2）．
由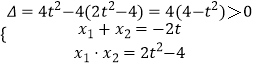 
，得|MN|= 
= 
．
．
所以， 
当且仅当t2=4﹣t2时取等号，即t2=2时取等号
所以△MNC面积的最大值为2．
此时直线l的方程 
【解析】（1）由椭圆长轴长是短轴长的两倍设出椭圆的方程，把点C的坐标代入椭圆方程可求解b，则椭圆的方程可求；（2）设出P点的坐标，写出直线CP和DP的斜率，由点P在椭圆上得到P点横纵坐标的关系式，代入斜率乘积的表达式整理可得直线CP和DP的斜率之积为定值；（3）由直线l平行于CD，设出直线l的斜截式方程，和椭圆方程联立后求出弦MN的长度，由点到直线的距离公式求出C到MN的距离，代入面积公式后利用基本不等式求最大值，并求出使面积最大时的直线l的方程．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
