题目内容
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.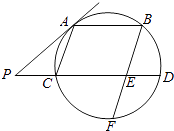
(1)求AC的长;
(2)试比较BE与EF的长度关系.
【答案】
(1)解:∵过A点的切线交DC的延长线于P,
∴PA2=PCPD,
∵PC=1,PA=2,
∴PD=4
又PC=ED=1,∴CE=2,
∵∠PAC=∠CBA,∠PCA=∠CAB,
∴△PAC∽△CBA,
∴ ![]() ,
,
∴AC2=PCAB=2,
∴AC= ![]() ;
;
(2)解: ![]() ,
,
由相交弦定理可得CEED=BEEF.
∵CE=2,ED=1,
∴EF= ![]() ,
,
∴EF=BE.)
【解析】(1)先求出CE,再证明△PAC∽△CBA,利用相似比,即可求AC的长;(2)由相交弦定理可得CEED=BEEF,求出EF,即可得出结论.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
PM2.5 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
(1)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(2)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(3)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.