题目内容
【题目】设函数f (x)=(x+1)lnx﹣a (x﹣1)在x=e处的切线与y轴相交于点(0,2﹣e).
(1)求a的值;
(2)函数f (x)能否在x=1处取得极值?若能取得,求此极值;若不能,请说明理由.
(3)当1<x<2时,试比较 ![]() 与
与 ![]() 大小.
大小.
【答案】
(1)解:f′(x)=lnx+ ![]() +1﹣a,
+1﹣a,
依题设得 ![]() =f′(e),即
=f′(e),即
e+1﹣a(e﹣1)﹣(2﹣e)=e ![]() ,
,
解得a=2
(2)解:函数f (x)不能在x=1处取得极值.
因为f′(x)=lnx+ ![]() ﹣1,记g(x)=ln x+
﹣1,记g(x)=ln x+ ![]() ﹣1,则g′(x)=
﹣1,则g′(x)= ![]() .
.
①当x>1时,g′(x)>0,所以g(x)在(1,+∞)是增函数,
所以g(x)>g(1)=0,所以f′(x)>0;
②当0<x<1时,g′(x)<0,所以g(x)在(0,1)是减函数,
所以g(x)>g(1)=0,即有f′(x)>0.
由①②得f (x)在(0,+∞)上是增函数,
所以x=1不是函数f (x)极值点.
(3)解:当1<x<2时, ![]() >
> ![]() ﹣
﹣ ![]() .
.
证明如下:由(2)得f (x)在(1,+∞)为增函数,
所以当x>1时,f(x)>f (1)=0.
即(x+1)lnx>2(x﹣1),所以 ![]() <
< ![]() .①
.①
因为1<x<2,所以0<2﹣x<1, ![]() >1,所以
>1,所以 ![]() <
< 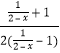 =
= ![]() ,
,
即﹣ ![]() <
< ![]() .②
.②
①+②得 ![]() ﹣
﹣ ![]() <
< ![]() +
+ ![]() =
= ![]()
【解析】

练习册系列答案
相关题目


