题目内容
3.已知实数t满足:t-$\frac{2}{t}$≥-1,求t值.分析 移项、通分,把原不等式化为等价的不等式组,求出解集即可.
解答 解:∵t-$\frac{2}{t}$≥-1,
∴t-$\frac{2}{t}$+1≥0,
即$\frac{{t}^{2}+t-2}{t}$≥0;
该不等式等价于$\left\{\begin{array}{l}{{t}^{2}+t-2≥0}\\{t>0}\end{array}\right.$或$\left\{\begin{array}{l}{{t}^{2}+t-2≤0}\\{t<0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{t≤-2或t≥1}\\{t>0}\end{array}\right.$或$\left\{\begin{array}{l}{-2≤t≤1}\\{t<0}\end{array}\right.$,
即t≥1或-2≤t<0;
∴t的取值范围是{t|t≥1或-2≤t<0}.
点评 本题考查了分式不等式的解法与应用问题,解题的关键是利用符号法则化为等价的不等式组,是基础题目.

练习册系列答案
相关题目
13.若f(x)=-x2+2ax与g(x)=$\frac{1}{x+a}$在区间[1,2]上都是减函数,则a的取值范围是( )
| A. | (-∞,1] | B. | [0,1] | C. | (-2,-1)∪(-1,1] | D. | (-∞,-2)∪(-1,1] |
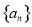 的通项公式
的通项公式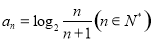 ,设其前
,设其前 项和为
项和为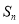 ,则使
,则使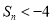 成立的自然数
成立的自然数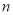 有( )
有( )