题目内容
14.在极坐标系中,已知直线l的极坐标方程为ρsin(θ+$\frac{π}{4}$)=1+$\sqrt{2}$,圆C的极坐标方程ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),直线l被圆C所截得的弦长为1.分析 把极坐标方程化为直角坐标方程,求出圆心到直线的距离,再利用弦长公式即可得出.
解答 解:由直线l的极坐标方程为ρsin(θ+$\frac{π}{4}$)=1+$\sqrt{2}$,展开化为$\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$=1+$\sqrt{2}$,即x+y-$\sqrt{2}$-2=0.
圆C的极坐标方程ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开化为${ρ}^{2}=2\sqrt{2}×\frac{\sqrt{2}}{2}(ρsinθ+ρcosθ)$,即x2+y2=2y+2x,配方为(x-1)2+(y-1)2=2.
∴圆心到直线l的距离d=$\frac{|1+1-\sqrt{2}-2|}{\sqrt{2}}$=1.
直线l被圆C所截得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$=$\sqrt{2-1}$=1.
故答案为:1.
点评 本题考查了把极坐标方程化为直角坐标方程、点到直线的距离公式、直线与圆相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.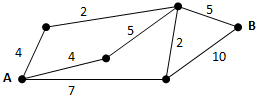 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
9.函数f(x)=x2+ax+2在区间[1,5]上至少有一个零点,则实数a的取值范围为( )
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
19.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则输出的S=$\frac{{a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+{a}_{5}+{a}_{6}}{6}$,其目的是求计算6名运动员三分球的平均数.

| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 | a1 | a2 | a3 | a4 | a5 | a6 |

4.已知等比数列的前n项和公式Sn=3(1-2n),则其首项a1和公比q分别为( )
| A. | a1=3,q=2 | B. | a1=-3,q=2 | C. | a1=3,q=-2 | D. | a1=-3,q=-2 |
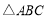 的一个内角为
的一个内角为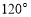 ,并且三边长构成公差为4的等差数列,则
,并且三边长构成公差为4的等差数列,则