题目内容
8.对于函数f(x)=log${\;}_{\frac{1}{2}}$(ax2-2x+4)(a∈R).(1)若f(x)的定义域是R,求a的取值范围;
(2)若f(x)的值域是R,求a的取值范围;
(3)若f(x)的值域是(-∞,1],求a的取值范围;
(4)若f(x)在(-∞,3]上为增函数,求a的取值范围.
分析 (1)根据f(x)的定义域为R,真数大于0恒成立,求出a的取值范围即可;
(2)当f(x)的值域是R时,真数取遍所有大于0的数,由此求出a的取值范围;
(3)当f(x)的值域是(-∞,1]时,真数大于或等于1恒成立,求出a的取值范围;
(4)当f(x)在(-∞,3]上为增函数时,应满足$\left\{\begin{array}{l}{a>0}\\{\frac{1}{a}≥3}\\{9a-6+4>0}\end{array}\right.$,由此求出a的取值范围.
解答 解:(1)∵函数f(x)=log${\;}_{\frac{1}{2}}$(ax2-2x+4)(a∈R),
当f(x)的定义域为R时,ax2-2x+4>0恒成立,
∴$\left\{\begin{array}{l}{a>0}\\{4-16a<0}\end{array}\right.$,
解得a>$\frac{1}{4}$,
∴a的取值范围是{a|a>$\frac{1}{4}$};
(2)当f(x)的值域是R时,有a=0时,满足条件;
又$\left\{\begin{array}{l}{a>0}\\{4-16a≥0}\end{array}\right.$,
解得0<a≤$\frac{1}{4}$,满足条件;
∴a的取值范围是{a|0≤a≤$\frac{1}{4}$};
(3)当f(x)的值域是(-∞,1]时,ax2-2x+4≥$\frac{1}{2}$恒成立,
∴ax2-2x+$\frac{7}{2}$≥0,
即$\left\{\begin{array}{l}{a>0}\\{4-14a≤0}\end{array}\right.$,
解得a≥$\frac{2}{7}$,
∴a的取值范围是{a|a≥$\frac{2}{7}$};
(4)当f(x)在(-∞,3]上为增函数时,
应满足$\left\{\begin{array}{l}{a>0}\\{\frac{1}{a}≥3}\\{9a-6+4>0}\end{array}\right.$,
解得$\frac{2}{9}$<a≤$\frac{1}{3}$,
∴a的取值范围是{a|$\frac{2}{9}$<a≤$\frac{1}{3}$}.
点评 本题考查了复合函数的定义域、值域和单调性的应用问题,是基础题目.

| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 | a1 | a2 | a3 | a4 | a5 | a6 |
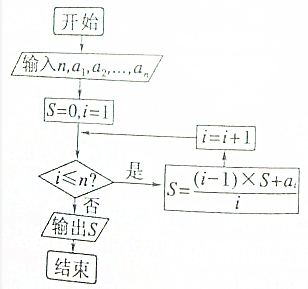
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
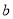 满足:
满足: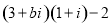 是纯虚数,则实数
是纯虚数,则实数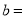 ( )
( )