题目内容
12.某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为$\frac{2}{π}$.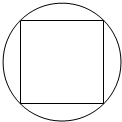
分析 根据几何概型的概率公式,分别求出正方形和圆的面积进行计算即可.
解答 解:设正方形的边长为a,则正方形的对角线为$\sqrt{2}$a,
即圆的直径2R=$\sqrt{2}$a,
则半径R=$\frac{\sqrt{2}}{2}$a,
则投中正方形区域的概率P=$\frac{{S}_{正方形}}{{S}_{圆}}$=$\frac{{a}^{2}}{π×(\frac{\sqrt{2}a}{2})^{2}}$=$\frac{2}{π}$,
故答案为:$\frac{2}{π}$
点评 本题主要考查几何概型的概率的计算,求出对应的面积是解决本题的关键.

练习册系列答案
相关题目
2.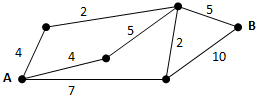 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
17.设集合A={1,2,3,4},B={1,2,3},x∈A且x∉B,则x=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.已知等比数列的前n项和公式Sn=3(1-2n),则其首项a1和公比q分别为( )
| A. | a1=3,q=2 | B. | a1=-3,q=2 | C. | a1=3,q=-2 | D. | a1=-3,q=-2 |