题目内容
18.若三点A(3,1)、B(-2,k)、C(8,1)能构成三角形,求实数k的取值范围.分析 因为A,B,C能构成三角形,故点A,B,C不共线,即 $\overrightarrow{AB}$,$\overrightarrow{AC}$不共线,得到关于k的不等式解之;
解答 解:因为三点A(3,1)、B(-2,k)、C(8,1)能构成三角形,$\overrightarrow{AB}$=(-2,k)-(3,1)=(-5,k-1),$\overrightarrow{AC}$=(8,1)-(3,1)=(5,0),
又A,B,C能构成三角形,故点A,B,C不共线,即$\overrightarrow{AB}$,$\overrightarrow{AC}$不共线,
所以5k-5≠0,解得k≠1;
实数k的取值范围:(-∞,1)∪(1,+∞).
点评 本题考查了向量的共线的充要条件的应用,三角形的解法;属于中档题.

练习册系列答案
相关题目
9.函数f(x)=x2+ax+2在区间[1,5]上至少有一个零点,则实数a的取值范围为( )
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |

 B.
B.
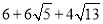 D.
D.