题目内容
11.已知直线x+y=0和圆(x-1)2+(y+3)2=4+a2,则它们的位置关系为相交.分析 依题意可知圆心为C(1,-3),半径为$\sqrt{4+{a}^{2}}$,利用点到直线的距离公式求得圆心C与l的距离d小于半径,可得直线和圆的位置关系.
解答 解:依题意可知圆心为C(1,-3),半径为$\sqrt{4+{a}^{2}}$,
C与l的距离为d=$\frac{|1-3|}{\sqrt{2}}$=$\sqrt{2}$<$\sqrt{4+{a}^{2}}$,
∴直线和圆的位置关系为相交,
故答案为:相交.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目
2.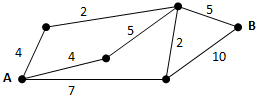 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
 如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆点表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿分开不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
19.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
如图是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则输出的S=$\frac{{a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+{a}_{5}+{a}_{6}}{6}$,其目的是求计算6名运动员三分球的平均数.

| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数 | a1 | a2 | a3 | a4 | a5 | a6 |

 的侧棱
的侧棱 底面
底面 ,
,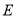 是棱
是棱 的中点,
的中点, 是
是 的中点,
的中点, .
.
 平面
平面 ;
; 的体积.
的体积.