题目内容
1.如图,⊙O的弦AB,CD交于点E,作EP∥CB,交AD的延长线于点P,PF为⊙O的切线,F为切点,求证:PE=PF.
分析 证明△DPE∽△EPA,可得PE2=PD•PA,利用切割线定理,可得PF2=PD•PA,即可得出结论.
解答 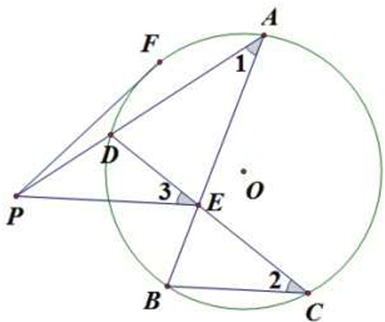 证明:∵EP∥CB,∴∠2=∠3,
证明:∵EP∥CB,∴∠2=∠3,
∵同弧上的圆周角相等,
∴∠1=∠2,
∴∠1=∠3,
在△DPE和△EPA中,∠DPE是共同角,
∴△DPE∽△EPA,
∴$\frac{PD}{PE}=\frac{PE}{PA}$,
∴PE2=PD•PA,
根据切割线定理PF2=PD•PA,
∴PE=PF.
点评 本题考查三角形相似的判断,考查切割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知a>b>0,那么下列不等式成立的是( )
| A. | -a>-b | B. | a+c<b+c | C. | a2>b2 | D. | $\frac{1}{a}$>$\frac{1}{b}$ |
11.如果a,b∈R,且ab<0那么下列不等式成立的是( )
| A. | |a+b|>|a-b| | B. | |a+b|<|a-b| | C. | |a-b|<||a|-|b|| | D. | |a-b|<|a|+|b| |
 一艘海轮从A处出发,以40n mile/h的速度沿南偏东40°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是10$\sqrt{2}$n mile.
一艘海轮从A处出发,以40n mile/h的速度沿南偏东40°方向直线航行,30min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是10$\sqrt{2}$n mile.