题目内容

1．设m是一个非负整数，m的个位数记作G（m），如G（2014）=4，G（17）=7，G（0）=0，称这样的函数为尾数函数．若a，b，c∈N，则给出的下列有关尾数函数的结论中：
①G（a+b）=G（a）+G（b）；②若a-b=10c，则G（a）=G（b）；
③G（a•b•c）=G（G（a）•G（b）•G（c））；④G（32015）=9．
以上正确的有（　　）
A．1个B．2个C．3个D．4个

分析 根据尾数函数的定义，分别对四个结论进行判断，即可得到答案．

解答 解：由题意得：
当a=b=5时，G（a+b）=0，G（a）+G（b）=10，故①错误，
G（a-b）=G（10c）=G（0）=0=G（a）-G（b），
∴G（a）=G（b），故②正确，
G[G（a）•G（b）•G（c）]=G（a•b•C），故③正确，
G（32015）=G[（10-1）1007•3]=G（7）=7，故④错误，
故选：B．

点评 本题考查了新定义问题，考查了求函数值问题，是一道基础题．

练习册系列答案
相关题目
1．阅读如图所示的程序框图，若输入m=6，则输出S等于（　　）
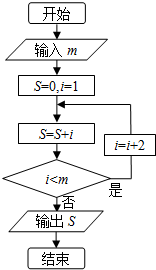
A．4B．9C．16D．25
2．下列不等式中，与不等式$\frac{x+8}{{{x^2}+2x+3}}$＜2解集相同的是（　　）
A．（x+8）（x2+2x+3）＜2B．x+8＜2（x2+2x+3）C．$\frac{1}{{{x^2}+2x+3}}$＜$\frac{2}{x+8}$D．$\frac{{{x^2}+2x+3}}{x+8}$＞$\frac{1}{2}$
9．在校英语节演讲比赛中，七位评委老师为某班选手打出的分数的茎叶图（如图所示），去掉一个最高分和一个最低分后，所剩数据的方差为$\frac{8}{5}$．
16．如图，在四棱台ABCD-A1B1C1D1中，DD1⊥底面ABCD，四边形ABCD为正方形，DD1=AD=2，A1B1=1，C1E∥平面ADD1A1．
（Ⅰ）证明：E为AB的中点；
（Ⅱ）求点E到平面ADC1的距离．
6．函数f（x）=sinx．
（1）令f1（x）=f′（x），fn+1（x）=fn′（x），（n∈N*），f2015（x）的解析式；
（2）若f（x）+1≥ax+cosx在[0，π]上恒成立，求实数a的取值范围；
（3）证明：f（$\frac{π}{2n+1}$）+f（$\frac{2π}{2n+1}$）+…+f（$\frac{（n+1）π}{2n+1}$）≥$\frac{{3\sqrt{2}（n+1）}}{4（2n+1）}$．
13．设函数f（x）=mx2-2mlnx-6+m，g（x）=x2-lnx
（1）当m=1时，求函数f（x）的单调区间及极值；
（2）若对于x∈[1，3]，f（x）＜0恒成立，求实数m的取值范围；
（3）若m＞0且对于任意x1∈[1，e]，任意x2∈[1，e]，不等式f（x1）＞g（x2）恒成立，求实数m的取值范围．
10．已知函数f（x）=（x-1）ex-x2．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求函数f（x）的单调区间；
（3）求函数f（x）在区间[0，k]（k＞0）上的最大值．
11．若经过点P（-1，1）的直线与圆x2+y2=2相切，则此直线在y轴上的截距是2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网