题目内容
如右图所示的曲线是以锐角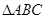 的顶点
的顶点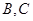 为
为
焦点,且经过点 的双曲线,若
的双曲线,若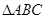 的内角的
的内角的
对边分别为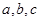 ,且
,且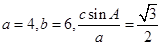 ,
,
则此双曲线的离心率为
 的顶点
的顶点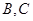 为
为焦点,且经过点
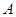 的双曲线,若
的双曲线,若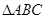 的内角的
的内角的对边分别为
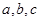 ,且
,且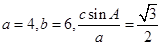 ,
,则此双曲线的离心率为
A.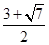 | B.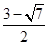 | C.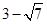 | D.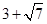 |

D
先根据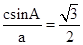 求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
解答:解: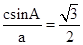 ?
?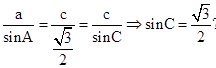 ,
,
∵C为锐角,
∴C=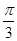 ,由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×
,由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×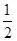 =28,
=28,
c=2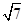 ,e=
,e=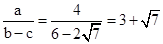 .
.
故选D
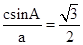 求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.解答:解:
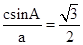 ?
?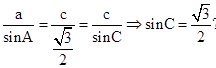 ,
,∵C为锐角,
∴C=
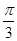 ,由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×
,由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×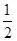 =28,
=28,c=2
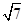 ,e=
,e=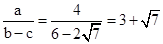 .
.故选D

练习册系列答案
相关题目
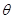 是三角形的一个内角,且
是三角形的一个内角,且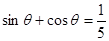 ,则方程
,则方程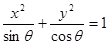 所表示的曲线为( ).
所表示的曲线为( ). 轴上的椭圆
轴上的椭圆 轴上的椭圆
轴上的椭圆 、
、 分别是椭圆C:
分别是椭圆C: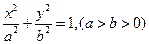 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 的周长是
的周长是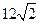 .
.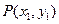 ,
,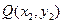 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段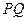 的中点为
的中点为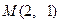 ,
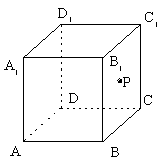
,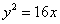 上的一点
上的一点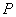 到
到 轴的距离为12,则
轴的距离为12,则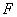 间的距离
间的距离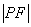 =______.
=______.
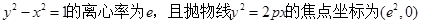 ,则p的值为( )
,则p的值为( ) 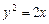 与过焦点的直线交于A、
与过焦点的直线交于A、 B
B 两点,则
两点,则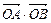 =" " .
=" " . (
(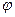 是参数)的左焦点,P是椭圆上对应于
是参数)的左焦点,P是椭圆上对应于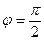 的点,那么线段AP的长是
的点,那么线段AP的长是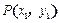 、
、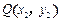 ,定义:
,定义: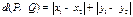 .已知点
.已知点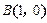 ,点M为直线
,点M为直线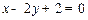 上的动点,则使
上的动点,则使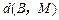 取最小值时点M坐标是.
取最小值时点M坐标是.