题目内容
抛物线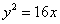 上的一点
上的一点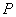 到
到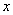 轴的距离为12,则
轴的距离为12,则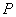 与焦点
与焦点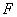 间的距离
间的距离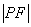 =______.
=______.
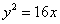 上的一点
上的一点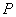 到
到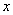 轴的距离为12,则
轴的距离为12,则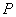 与焦点
与焦点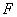 间的距离
间的距离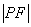 =______.
=______.13
分析:先把点P的纵坐标代入抛物线方程求得点P的横坐标,进而根据抛物线的定义求得答案.
解:依题意可知点P的纵坐标|y|=12,代入抛物线方程求得x=9
抛物线的准线为x=-4,
根据抛物线的定义可知点P与焦点F间的距离9+4=13
故答案为13

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
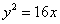 上的一点
上的一点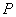 到
到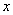 轴的距离为12,则
轴的距离为12,则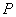 与焦点
与焦点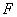 间的距离
间的距离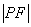 =______.
=______.
 名校课堂系列答案
名校课堂系列答案