题目内容
【题目】已知![]()
(1)求![]() 的值;
的值;
(2)当x∈(﹣t,t](其中t∈(﹣1,1),且t为常数)时,f(x)是否存在最小值,如果存在求出最小值;如果不存在,请说明理由;
(3)当f(x﹣2)+f(4﹣3x)≥0时,求满足不等式f(x﹣2)+f(4﹣3x)≥0的x的范围.
【答案】解:(1)令![]()
![]() ,解得﹣1<x<1,即函数f(x)的定义域为(﹣1,1),关于原点对称.
,解得﹣1<x<1,即函数f(x)的定义域为(﹣1,1),关于原点对称.
又f(﹣x)=loga![]() =loga(
=loga(![]() )-1=﹣loga
)-1=﹣loga![]() =﹣f(x),
=﹣f(x),
所以f(x)为奇函数,
所以![]() =
=![]() ﹣
﹣![]() =0.
=0.
(2)设﹣1<x1<x2<1,
则![]() ﹣
﹣![]() =
=![]() .
.
因为﹣1<x1<x2<1,
所以![]() ﹣
﹣![]() >0,即
>0,即![]() >
>![]() .
.
所以![]() 在(﹣1,1)上为减函数,也在(﹣t,t]上为减函数,
在(﹣1,1)上为减函数,也在(﹣t,t]上为减函数,
①当a>1时,y=logat单调递增,t=![]() 单调递减,所以y=loga
单调递减,所以y=loga![]() 在(﹣t,t]上单调递减,
在(﹣t,t]上单调递减,
此时f(x)存在最小值为f(t)=log![]() .
.
②当0<a<1时,y=logat单调递减,t=![]() 单调递减,所以y=loga
单调递减,所以y=loga![]() 在(﹣t,t]上单调递增,
在(﹣t,t]上单调递增,
此时f(x)不存在最小值.
综①②知,当a>1时,f(x)存在最小值为f(t)=loga![]() .
.
(3)f(x﹣2)+f(4﹣3x)≥0可化为f(x﹣2)≥﹣f(4﹣3x),
由(1)知f(x)为奇函数,所以f(x﹣2)≥f(3x﹣4),
①当a>1时,由(2)知f(x)在(﹣1,1)上为减函数,
所以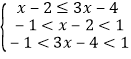 ,解得1<x<
,解得1<x<![]() .
.
②当0<a<1时,由(2)知f(x)在(﹣1,1)上为增函数,
所以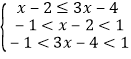 ,解得为.
,解得为.
综①②得满足不等式f(x﹣2)+f(4﹣3x)≥0的x的范围为:(1,![]() ).
).
【解析】(1)由所求表达式的特点知,可判断函数的奇偶性;
(2)根据复合函数单调性的判定方法判断f(x)的单调性,由单调性可讨论f(x)的最小值情况;
(3)利用f(x)的奇偶性把f(x﹣2)+f(4﹣3x)≥0可化为f(x﹣2)≥f(3x﹣4),再利用f(x)的单调性即可解出不等式.
【考点精析】本题主要考查了函数单调性的性质和函数的值的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.

