题目内容
【题目】已知平面上的线段![]() 及点
及点![]() ,任取
,任取![]() 上的一点
上的一点![]() ,线段
,线段![]() 长度的最小值称为点
长度的最小值称为点![]() 到线段
到线段![]() 的距离,记为
的距离,记为![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() 满足
满足![]() ,则
,则![]() 关于
关于![]() 的函数解析式为________
的函数解析式为________
【答案】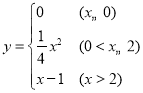
【解析】
寻找平面内到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离相等的点的轨迹,当
的距离相等的点的轨迹,当![]() 时,
时,![]() 轴上的点到线段
轴上的点到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,当
的距离,当![]() 时,点
时,点![]() 到线段
到线段![]() 的距离即为到点
的距离即为到点![]() 的距离,到点
的距离,到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离相等的点的轨迹为抛物线,当
的距离相等的点的轨迹为抛物线,当![]() 时,满足到线段
时,满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离即为到点
的距离即为到点![]() 与到点
与到点![]() 的距离相等点,从而求出
的距离相等点,从而求出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
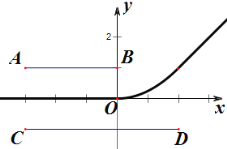
根据题意画出线段![]() 与线段
与线段![]() ,
,
![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 满足到线段
满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,
的距离,
当![]() 时,
时,![]() 轴上的点到线段
轴上的点到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,故
的距离,故![]() ,
,
当![]() 时,点
时,点![]() 到线段
到线段![]() 的距离即为到点
的距离即为到点![]() 的距离,到点
的距离,到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离相等的点的轨迹为抛物线,
的距离相等的点的轨迹为抛物线,
根据抛物线的定义可知点![]() 是抛物线的焦点,
是抛物线的焦点,![]() 是准线,则
是准线,则![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
当![]() 时,满足到线段
时,满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离即为到点
的距离即为到点![]() 与到点
与到点![]() 的距离相等点,在平面内到两定点距离相等的点即为线段
的距离相等点,在平面内到两定点距离相等的点即为线段![]() 的垂直平分线,
的垂直平分线,
![]() 点
点![]() 的轨迹为
的轨迹为![]() ,
,
![]() 关于
关于![]() 的函数解析式为:
的函数解析式为: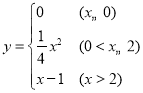 .
.
故答案为: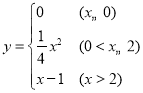 .
.

练习册系列答案
相关题目