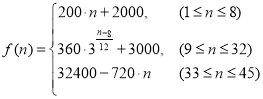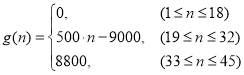题目内容
【题目】用一个长为![]() ,宽为
,宽为![]() 的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
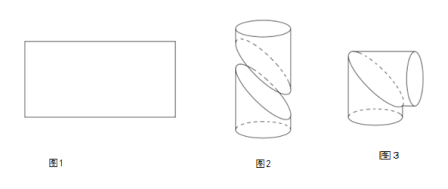
(1)求直角圆形弯管(图3)的体积;
(2)求斜截面椭圆的焦距;
(3)在相应的图1中建立适当的坐标系,使所画的曲线的方程为![]() ,求出方程并画出大致图像;
,求出方程并画出大致图像;
【答案】(1)![]() ; (2)2; (3)见解析;
; (2)2; (3)见解析;
【解析】
(1)直角圆形弯管的体积即为圆柱的体积,要使直角圆形弯管的体积最大,可取圆柱的高为![]() ,半径为1,计算可得所求体积;
,半径为1,计算可得所求体积;
(2)求得![]() ,以矩形的下边的中点为
,以矩形的下边的中点为![]() ,下边所在直线为
,下边所在直线为![]() 轴,建立所示的直角坐标系,设出曲线方程,应用周期性和对称性,求得方程,再由椭圆的长轴和短轴的关系,可得焦距;
轴,建立所示的直角坐标系,设出曲线方程,应用周期性和对称性,求得方程,再由椭圆的长轴和短轴的关系,可得焦距;
(3)由(2)可得方程,画出方程表示的曲线.
解:(1)直角圆形弯管的体积即为圆柱的体积,
要使直角圆形弯管的体积最大,
可取圆柱的高为![]() ,
,
那么圆柱的底面半径![]() 为
为![]() ,
,
即有直角圆形弯管(图![]() 的体积为
的体积为![]() ;
;
(2)由图2可得椭圆短轴长为![]() ,即
,即![]() ,
,
可以矩形的下边的中点为![]() ,
,
下边所在直线为![]() 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,
由周期为![]() ,可得
,可得![]() ,
,
再由![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
又![]() ,可得
,可得![]() ,
,
所求方程为![]() ,
,![]() ,
,
可得![]() ,
,
解得![]() ,
,![]() ,
,
可得椭圆的焦距为2;
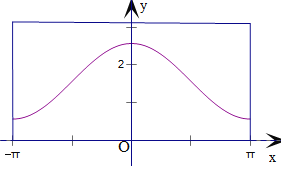
(3)由(2)可得,方程为![]() ,
,![]() ,
,
图象如右图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目