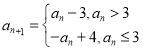题目内容
【题目】设点![]() 是边长为2的正三角形
是边长为2的正三角形![]() 的三边上的动点,则
的三边上的动点,则![]() 的取值范围为______
的取值范围为______
【答案】![]()
【解析】
以![]() 中点为坐标原点,建立平面直角坐标,写出各个点的坐标,分别讨论点
中点为坐标原点,建立平面直角坐标,写出各个点的坐标,分别讨论点![]() 在
在![]() 上.写出
上.写出![]() 点坐标,由平面向量的坐标表示分别表示出
点坐标,由平面向量的坐标表示分别表示出![]() ,结合平面向量数量积的坐标运算求得
,结合平面向量数量积的坐标运算求得![]() ,再根据二次函数的性质即可求得取值范围.
,再根据二次函数的性质即可求得取值范围.
根据题意,以![]() 中点为坐标原点,建立如图所示的平面直角坐标:
中点为坐标原点,建立如图所示的平面直角坐标:
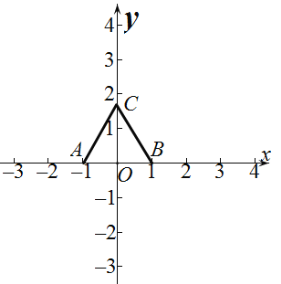
正三角形![]() 的边长为2,则
的边长为2,则![]() ,点
,点![]() 是
是![]() 三边上的动点,
三边上的动点,
![]() ,当
,当![]() 在线段
在线段![]() 上时,设
上时,设![]() ,
,
则![]()
所![]()
![]()
![]()

![]()
所以当![]() 时取得最小值为
时取得最小值为![]() ;当
;当![]() 时取得最大值为2.
时取得最大值为2.
![]() ,当
,当![]() 在线段
在线段![]() 上时,
上时,
直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
则![]() ,
,
所![]()
![]()
![]()
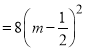
![]()
所以当![]() 时取得最小值为0;当
时取得最小值为0;当![]() 或
或![]() 时取得最大值为2.
时取得最大值为2.
![]() ,当
,当![]() 在线段
在线段![]() 上时,
上时,
直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,
则![]() ,
,
所![]() ,
,
![]() ,
,
![]() ,
,

![]() ,
,
所以当![]() 时取得最小值为
时取得最小值为![]() ;当
;当![]() 时取得最大值为2.
时取得最大值为2.
综上可知,![]() 的取值范围为
的取值范围为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目