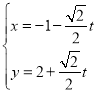题目内容
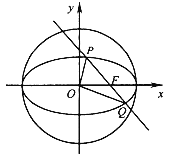
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).在以
为参数).在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,曲线![]() :
:![]() 的焦点
的焦点![]() 的极坐标为
的极坐标为![]() .
.
(1)求常数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的大小.
的大小.
【答案】(1)8;(2)![]() 或
或![]() .
.
【解析】
(1)曲线C的极坐标方程化为直角坐标方程知曲线C为抛物线,焦点![]() 的极坐标方程转化为直角坐标方程即可求得
的极坐标方程转化为直角坐标方程即可求得![]() ;(2)将直线
;(2)将直线![]() 的参数方程代入
的参数方程代入![]() 整理得到关于t的一元二次方程,根据韦达定理用
整理得到关于t的一元二次方程,根据韦达定理用![]() 表示出
表示出![]() 、
、![]() ,由
,由![]() 得
得![]() ,三个方程联立即可求出
,三个方程联立即可求出![]() .
.
(1)曲线![]() 方程可化为
方程可化为![]() ,其直角坐标方程为
,其直角坐标方程为![]() .
.
又焦点![]() 的直角坐标为
的直角坐标为![]() ,
,
所以![]() ,解得
,解得![]() .
.
(2)将直线![]() 的参数方程代入
的参数方程代入![]() ,并整理得
,并整理得![]() ,
,
其中![]() 恒成立,且
恒成立,且![]() ①,
①,![]() ②,
②,
由![]() 得
得![]() ,结合①得
,结合①得![]() ,
,![]() .
.
代入②得![]() ,解得
,解得![]() .
.
又因为![]() ,所以
,所以![]() 的大小为
的大小为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为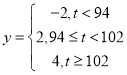 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.