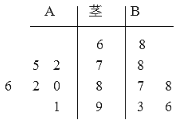
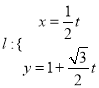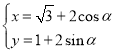题目内容
【题目】已知圆![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,证明:直线
两点,证明:直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为定值.
的斜率之和为定值.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)由PF的中垂线可得GP=GF,而GP+GE=PE=4,进而可得G的轨迹为椭圆;且可得F,E为椭圆的焦点,PE的长为长轴长,进而求出椭圆的方程;(2)设直线MN的方程,与椭圆联立求出两根之和及两根之积,进而求出直线SM,SN的斜率之和,将之和及之积代入,由由于Q在直线上,可得参数的关系,进而可得斜率之和为定值.
(1)因为点![]() 在
在![]() 的垂直平分线上,所以
的垂直平分线上,所以![]() .
.
而![]() ,
,
所以动点![]() 满足
满足![]() ,
,
椭圆定义可知,![]() 点在以
点在以![]() 、
、![]() 为焦点的椭圆上,且
为焦点的椭圆上,且![]() ,
,
所以![]() ,
,
所以曲线![]() 的方程为
的方程为![]() .
.
(2)由题意知直线![]() 斜率存在.
斜率存在.
设其方程为![]() ,
,![]() ,
,![]() ,
,
联立方程组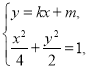 代入消元并整理得:
代入消元并整理得:
![]() ,
,
则![]() ,
,![]() .
.
![]() ,将直线方程代入,整理得:
,将直线方程代入,整理得:
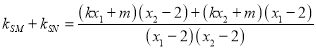
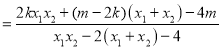 ,
,
韦达定理代入化简得:![]() .
.
因为直线![]() 过点
过点![]() ,所以
,所以![]() ,
,
代入![]() ,得
,得![]() .
.

【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费(元) |
|
|
|
|
|
随机调查了该险种的![]() 名续保人在一年内的出险情况,得到下表:
名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
|
|
将所抽样本的频率视为概率.
(1)求本年度续保人保费的平均值的估计值;
(2)按保险合同规定,若续保人在本年度内出险![]() 次,则可获得赔付
次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(3)续保人原定约了保险公司的销售人员在上午![]() 之间上门签合同,因为续保人临时有事,外出的时间在上午
之间上门签合同,因为续保人临时有事,外出的时间在上午![]() 之间,请问续保人在离开前见到销售人员的概率是多少?
之间,请问续保人在离开前见到销售人员的概率是多少?