题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
【答案】19. 解①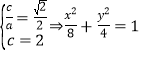
②设![]()
![]()
由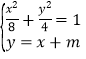
![]()
![]()
![]()
又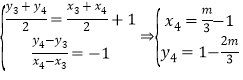 在
在![]() 上
上
![]()
![]()
![]() 或
或![]()
经检验解题
![]() 或
或![]()
【解析】
本试题主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的运用。
(1)由题意,得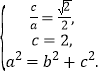 得到a,b,c的值。得到椭圆的方程。
得到a,b,c的值。得到椭圆的方程。
(2)设点A、B的坐标分别为(x1,y1),(x2, y2),线段AB的中点为M(x0,y0),
由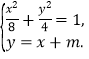 消y得,3x2+4mx+2m2-8=0结合韦达定理,和判别式得到参数m值。
消y得,3x2+4mx+2m2-8=0结合韦达定理,和判别式得到参数m值。
解:(1) 由题意,得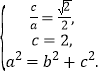 ………………………………………………3分
………………………………………………3分
解得![]() ∴椭圆C的方程为
∴椭圆C的方程为![]() .…………………………………………6分
.…………………………………………6分
(2) 设点A、B的坐标分别为(x1,y1),(x2, y2),线段AB的中点为M(x0,y0),
由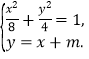 消y得,3x2+4mx+2m2-8=0,……………………………………………8分
消y得,3x2+4mx+2m2-8=0,……………………………………………8分
Δ=96-8m2>0,∴-2![]() <m<2
<m<2![]() .
.
∴![]()
![]() .………………………………………12分
.………………………………………12分
∵点M(x0,y0)在圆x2+y2=1上,
![]() ,
,![]() .………………………………………………… 14分
.………………………………………………… 14分

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

