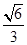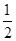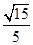题目内容
如图,正四棱锥S-ABCD的侧棱长为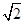 ,底面边长为
,底面边长为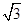 ,E为SA的中点,则异面直线BE与SC所成的角是( ).
,E为SA的中点,则异面直线BE与SC所成的角是( ).
| A.30° | B.45° | C.60° | D.90° |
C
解析

练习册系列答案
相关题目
三棱锥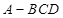 中,
中, 分别是
分别是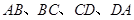 的中点,则四边形
的中点,则四边形 是( )
是( )
| A.菱形 | B.矩形 | C.梯形 | D.正方形 |
已知两条直线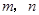 ,两个平面
,两个平面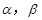 .下面四个命题中不正确的是( )
.下面四个命题中不正确的是( )
A. |
B.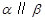 , ,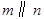 , ,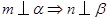 ; ; |
C.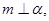 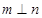 , ,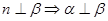 |
D.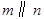 , ,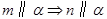 |
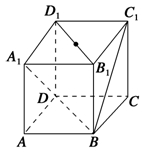
如图所示,在正方体 中,点
中,点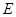 是棱
是棱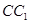 上的一个动点,平面
上的一个动点,平面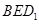 交棱
交棱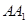 于点
于点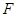 .则下列命题中假命题是( )
.则下列命题中假命题是( )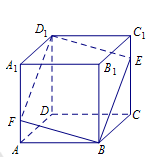
A.存在点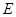 ,使得 ,使得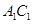 //平面 //平面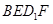 |
B.存在点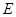 ,使得 ,使得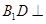 平面 平面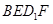 |
C.对于任意的点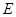 ,平面 ,平面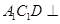 平面 平面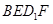 |
D.对于任意的点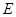 ,四棱锥 ,四棱锥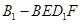 的体积均不变 的体积均不变 |
已知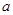 、b为两条直线,
、b为两条直线,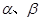 为两个平面,下列四个命题:
为两个平面,下列四个命题:
①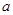 ∥b,
∥b,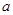 ∥
∥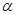
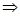 b∥
b∥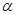 ; ②
; ②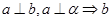 ∥
∥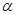
③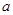 ∥
∥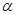 ,
,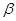 ∥
∥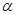
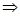
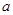 ∥
∥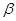 ④
④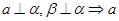 ∥
∥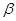
其中不正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知空间中有三条线段AB,BC和CD,且∠ABC=∠BCD,那么直线AB与CD的位置关系是( )
| A.AB∥CD |
| B.AB与CD异面 |
| C.AB与CD相交 |
| D.AB∥CD或AB与CD异面或AB与CD相交 |
如图,正方体ABCD-A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=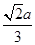 ,则MN与平面BB1C1C的位置关系是( ).
,则MN与平面BB1C1C的位置关系是( ).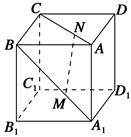
| A.相交 | B.平行 | C.垂直 | D.不能确定 |
如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有 ( ).
| A.AP⊥△PEF所在平面 |
| B.AG⊥△PEF所在平面 |
| C.EP⊥△AEF所在平面 |
| D.PG⊥△AEF所在平面 |
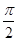 ,则BC1与平面BB1D1D所成角的正弦值为( ).
,则BC1与平面BB1D1D所成角的正弦值为( ).