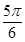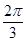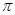题目内容
已知两条直线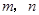 ,两个平面
,两个平面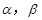 .下面四个命题中不正确的是( )
.下面四个命题中不正确的是( )
A. |
B.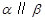 , ,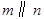 , ,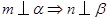 ; ; |
C.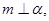 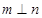 , ,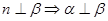 |
D.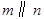 , ,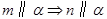 |
D
解析试题分析:选项 正确
正确
选项 正确
正确
选项 过空间任一点
过空间任一点 作
作 平行线
平行线 分别交平面
分别交平面 于点
于点 因为
因为 垂直,所以
垂直,所以 必相交,能确定一个平面
必相交,能确定一个平面 .设
.设 与平面
与平面 的交线交于点
的交线交于点 则由
则由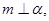
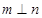
 得四边形
得四边形 为矩形,而
为矩形,而 为
为 平面角,所以
平面角,所以 正确
正确
选项 或
或 不正确
不正确
考点:直线与平面、平面与平面平行与垂直关系判定与性质定理综合应用.

练习册系列答案
相关题目
设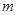 ,
, 是两条不同的直线,
是两条不同的直线,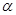 ,
,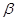 ,
,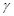 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题:
①若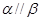 ,
,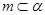 ,
,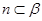 ,则
,则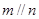 ;
;
②若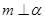 ,
,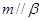 ,则
,则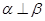 ;
;
③ 若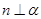 ,
,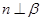 ,
,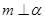 ,则
,则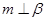 ;
;
④ 若 ,
,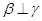 ,
,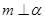 ,则
,则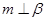 .
.
其中错误命题的序号是( )
| A.①④ | B.①③ | C.②③④ | D.②③ |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等,则这两条直线平行 |
| B.若一个平面内有不共线的三点到另一个平面的距离相等,则这两个平面平行 |
| C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| D.若两个平面都垂直于第三个平面,则这两个平面平行 |
设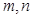 是不同的直线,
是不同的直线,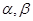 是不同的平面,下列命题中正确的是( )
是不同的平面,下列命题中正确的是( )
A.若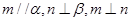 ,则 ,则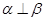 |
B.若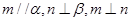 ,则 ,则 |
C.若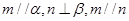 ,则 ,则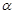 ⊥ ⊥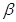 |
D.若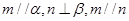 ,则 ,则 |
已知面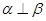 ,
, ,直线
,直线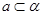 ,直线
,直线 ,
, 斜交,则( )
斜交,则( )
A.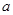 和 和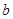 不垂直但可能平行 不垂直但可能平行 | B.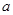 和 和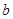 可能垂直也可能平行 可能垂直也可能平行 |
C.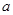 和 和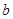 不平行但可能垂直 不平行但可能垂直 | D.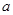 和 和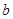 既不垂直也不平行 既不垂直也不平行 |
设 是两个不同的平面,
是两个不同的平面, 是一条直线,则下列命题正确的是( )
是一条直线,则下列命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
正四棱锥S-ABCD的侧棱长为 ,底面边长为
,底面边长为 ,E为SA的中点,则异面直线BE和SC所成的角为( ).
,E为SA的中点,则异面直线BE和SC所成的角为( ).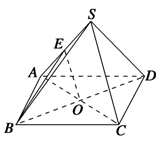
| A.30° | B.45° | C.60° | D.90° |
如图,正四棱锥S-ABCD的侧棱长为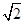 ,底面边长为
,底面边长为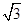 ,E为SA的中点,则异面直线BE与SC所成的角是( ).
,E为SA的中点,则异面直线BE与SC所成的角是( ).
| A.30° | B.45° | C.60° | D.90° |
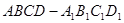 的棱长为
的棱长为 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )