题目内容
已知F是抛物线y2=4x的焦点，A，B是抛物线上两点，△AFB是正三角形，则该正三角形的边长为______．
y2=4x的焦点F（1，0）
等边三角形的一个顶点位于抛物线y2=4x的焦点，另外两个顶点在抛物线上，
则等边三角形关于x轴对称，两个边的斜率k=±tan30°=±
，其方程为：y=±
（x-1），
与抛物线y2=4x联立，可得
（x-1）2=4x
∴x=7±4
，
当x=7+4
时，y=±2（2+
），∴等边三角形的边长为8+4
；
当x=7-4
时，y=±2（2-
），∴等边三角形的边长为8-4
；
故答案为：8±4
；
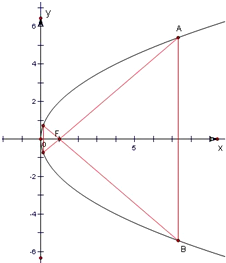
等边三角形的一个顶点位于抛物线y2=4x的焦点，另外两个顶点在抛物线上，
则等边三角形关于x轴对称，两个边的斜率k=±tan30°=±
| ||
| 3 |
| ||
| 3 |
与抛物线y2=4x联立，可得
| 1 |
| 3 |
∴x=7±4
| 3 |
当x=7+4
| 3 |
| 3 |
| 3 |
当x=7-4
| 3 |
| 3 |
| 3 |
故答案为：8±4
| 3 |
练习册系列答案
中考解读考点精练系列答案
相关题目
