题目内容
已知抛物线C:y2=2px(p>0)上一动点M,设M到抛物线C外一定点A(6,12)的距离为d1,M到定直线l:x=-p的距离为d2,若d1+d2的最小值为14,则抛物线C的方程为______.
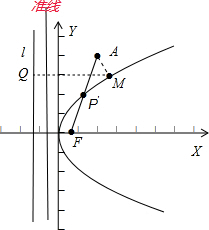
由于抛物线C:y2=2px(p>0)上一动点M,如图示,
则M到抛物线的焦点F(
,0)的距离等于M到准线:x=-
p的距离,
又由于M到定直线l:x=-p的距离为M到准线:x=-
p的距离与
的和,
则d2=MQ=MF+
,
故d1+d2=MA+MF+
的最小值为14,
由图知,当M与P′重合时,取最小值14,
则14=AF+
=
+
,解得p=2,
则抛物线C的方程为y2=4x.
故答案为:y2=4x.
则M到抛物线的焦点F(
| p |
| 2 |
| 1 |
| 2 |
又由于M到定直线l:x=-p的距离为M到准线:x=-
| 1 |
| 2 |
| p |
| 2 |
则d2=MQ=MF+
| p |
| 2 |
故d1+d2=MA+MF+
| p |
| 2 |
由图知,当M与P′重合时,取最小值14,
则14=AF+
| p |
| 2 |
(6-
|
| p |
| 2 |
则抛物线C的方程为y2=4x.
故答案为:y2=4x.


练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
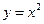 上到直线
上到直线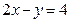 的距离最短的点的坐标是( )
的距离最短的点的坐标是( )


