Question

【题目】已知函数=

(1)写出该函数的单调区间;

(2)若函数=-m恰有3个不同零点,求实数m的取值范围;

(3)若≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.

Answer 1

【答案】(1) f(x)的单调递减区间是(0,1),单调递增区间是(-∞,0)及(1,+∞) (2) 实数m的取值范围为 (3) n的取值范围是(-∞,-2]∪{0}∪[2,+∞)

【解析】

（1）x≤0的图象部分可由图象变换作出；x＞0的部分为抛物线的一部分．
（2）数形结合法：转化为直线y=m与函数f（x）的图象有三个交点．
（3）将f（x）≤n2-2bn+1对所有x∈[-1，1]恒成立，转化为[f（x）]max≤n2-2bn+1即n2-2bn≥0在b∈[-1，1]恒成立，从而建立关于n的不等关系，求出n的取值范围．

(1)函数f(x)的图象如图所示,

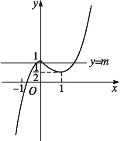
则函数f(x)的单调递减区间是(0,1),单调递增区间是(-∞,0)及(1,+∞)

(2)作出直线y=m,函数g(x)=f(x)-m恰有3个不同零点等价于直线y=m与函数f(x)的图象恰有三个不同交点.

根据函数f(x)=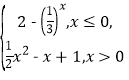的图象,

且f(0)=1,f(1)=,

∴m∈.

故实数m的取值范围为

(3)∵f(x)≤n2-2bn+1对所有x∈[-1,1]恒成立,

∴[f(x)]max≤n2-2bn+1,

又[f(x)]max=f(0)=1,

∴n2-2bn+1≥1,即n2-2bn≥0在b∈[-1,1]上恒成立.令h(b)=-2nb+n2,

∴h(b)=-2nb+n2在b∈[-1,1]上恒大于等于0.

∴

即

由①得

解得n≥0或n≤-2.

同理由②得n≤0或n≥2.

∴n∈(-∞,-2]∪{0}∪[2,+∞).

故n的取值范围是(-∞,-2]∪{0}∪[2,+∞)