题目内容
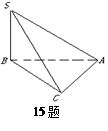
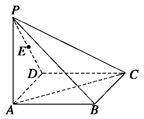
(本小题14分)如图所示,在四棱锥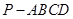 中,底面
中,底面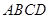 为矩形,侧棱
为矩形,侧棱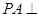 底面
底面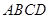 ,
,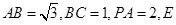 为
为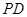 的中点.
的中点.
(1)求直线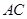 与
与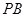 所成角的余弦值;
所成角的余弦值;
(2)在侧面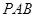 内找一点
内找一点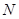 ,使
,使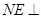 平面
平面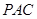 ,并分别求出点
,并分别求出点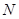 到
到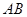 和
和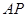 的距离.
的距离.
 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱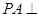 底面
底面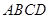 ,
,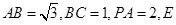 为
为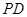 的中点.
的中点.(1)求直线
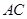 与
与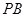 所成角的余弦值;
所成角的余弦值;(2)在侧面
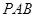 内找一点
内找一点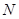 ,使
,使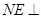 平面
平面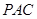 ,并分别求出点
,并分别求出点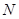 到
到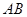 和
和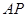 的距离.
的距离.
解 方法一 (1)建立如图所示的空间直角坐标系,
则A、B、C、D、P、E的坐标为A(0,0,0),B(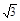 ,0,0)、C(
,0,0)、C(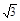 ,1,0)、D(0,1,0)、P(0,0,2)、
,1,0)、D(0,1,0)、P(0,0,2)、
E(0,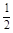 ,1),从而
,1),从而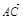 =(
=(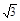 ,1,0),
,1,0),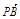 =(
=(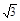 ,0,-2).
,0,-2).
设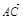 与
与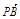 的夹角为
的夹角为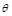 ,则cos
,则cos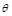 =
= =
=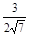 =
=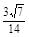 ,
,
∴AC与PB所成角的余弦值为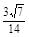 ……………………………………7分
……………………………………7分
(2)由于N点在侧面PAB内,故可设N点坐标为(x,0,z),则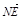 =(-x,
=(-x,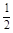 ,1-z),由NE⊥平面PAC可得
,1-z),由NE⊥平面PAC可得
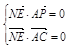 ,即
,即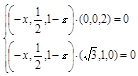 ,化简得
,化简得 ,∴
,∴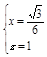
即N点的坐标为(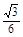 ,0,1),
,0,1),
从而N点到AB、AP的距离分别为1,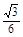 …………………14分
…………………14分
方法二 (1)设AC∩BD=O,
连接OE,AE,BD,则OE∥PB,
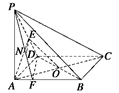
∴∠EOA即为AC与PB所成的角或其补角.
在△AOE中,AO=1,OE=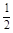 PB=
PB=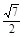 ,AE=
,AE=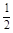 PD=
PD=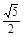 ,
,
∴由余弦定理得cos∠EOA=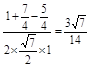 ,
,
即AC与PB所成角的余弦值为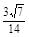 .
.
(2)在平面ABCD内过D作AC的垂线交AB于F,则∠ADF=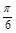 .连接PF,则在Rt△ADF中,DF=
.连接PF,则在Rt△ADF中,DF=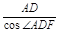 =
=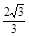 ,AF=AD·tan∠ADF=
,AF=AD·tan∠ADF=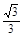 .
.
设N为PF的中点,连接NE,则NE∥DF.
∵DF⊥AC,DF⊥PA,
∴DF⊥平面PAC,从而NE⊥平面PAC.
∴N点到AB的距离为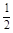 AP=1,N点到AP的距离为
AP=1,N点到AP的距离为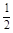 AF=
AF=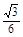 .
.
则A、B、C、D、P、E的坐标为A(0,0,0),B(
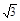 ,0,0)、C(
,0,0)、C(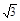 ,1,0)、D(0,1,0)、P(0,0,2)、
,1,0)、D(0,1,0)、P(0,0,2)、E(0,
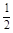 ,1),从而
,1),从而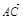 =(
=(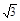 ,1,0),
,1,0),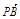 =(
=(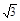 ,0,-2).
,0,-2).设
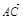 与
与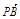 的夹角为
的夹角为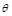 ,则cos
,则cos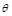 =
= =
=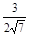 =
=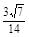 ,
,∴AC与PB所成角的余弦值为
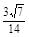 ……………………………………7分
……………………………………7分(2)由于N点在侧面PAB内,故可设N点坐标为(x,0,z),则
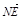 =(-x,
=(-x,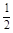 ,1-z),由NE⊥平面PAC可得
,1-z),由NE⊥平面PAC可得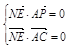 ,即
,即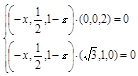 ,化简得
,化简得 ,∴
,∴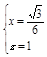
即N点的坐标为(
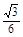 ,0,1),
,0,1),从而N点到AB、AP的距离分别为1,
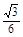 …………………14分
…………………14分方法二 (1)设AC∩BD=O,
连接OE,AE,BD,则OE∥PB,

∴∠EOA即为AC与PB所成的角或其补角.
在△AOE中,AO=1,OE=
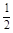 PB=
PB=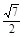 ,AE=
,AE=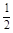 PD=
PD=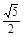 ,
,∴由余弦定理得cos∠EOA=
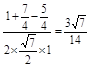 ,
,即AC与PB所成角的余弦值为
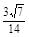 .
.(2)在平面ABCD内过D作AC的垂线交AB于F,则∠ADF=
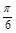 .连接PF,则在Rt△ADF中,DF=
.连接PF,则在Rt△ADF中,DF=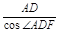 =
=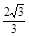 ,AF=AD·tan∠ADF=
,AF=AD·tan∠ADF=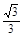 .
.设N为PF的中点,连接NE,则NE∥DF.
∵DF⊥AC,DF⊥PA,
∴DF⊥平面PAC,从而NE⊥平面PAC.
∴N点到AB的距离为
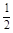 AP=1,N点到AP的距离为
AP=1,N点到AP的距离为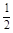 AF=
AF=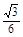 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是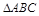 所在平面外的一点,且
所在平面外的一点,且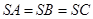 ,若
,若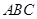 内的射影落在
内的射影落在 ABC外部,则
ABC外部,则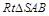 的两边
的两边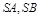 互相垂直,且
互相垂直,且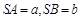 ,则
,则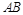 边上的高
边上的高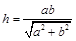 ;现在把结论类比到空间:三棱锥
;现在把结论类比到空间:三棱锥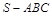 的三条侧棱
的三条侧棱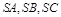 两两相互垂直,
两两相互垂直,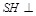 平面
平面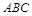 ,且
,且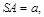
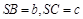 ,则点
,则点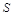 到平面
到平面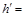
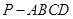 中,
中,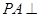 底面
底面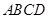 ,
,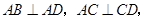
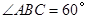 ,
,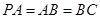 ,
,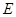 是
是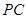 的中点.
的中点.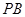 和平面
和平面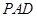 所成的角的大小;
所成的角的大小;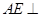 平面
平面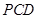 ;
;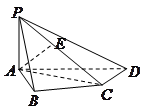
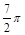
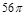
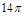
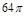
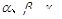 表示三个不同的平面,有下列四个命题:
表示三个不同的平面,有下列四个命题: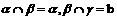 且
且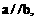 则
则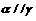 ;
;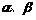 外,
外,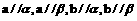 ,则
,则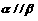 ;
;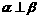 ,
,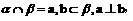 则
则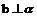 ;
;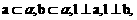 则
则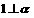 .
.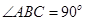 ,AD=a,BC=2a,
,AD=a,BC=2a,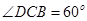 ,在平面ABCD内,过C作
,在平面ABCD内,过C作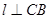 ,以
,以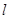 为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。
为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。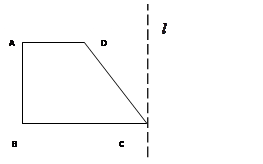
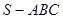 中,
中, 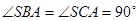 , △
, △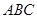 是斜边
是斜边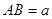 的等腰直角三角形, 则以下结论中: ① 异面直线
的等腰直角三角形, 则以下结论中: ① 异面直线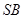 与
与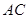 所成的角为
所成的角为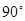 ; ② 直线
; ② 直线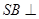 平面
平面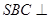 面
面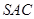 ; ④ 点
; ④ 点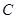 到平面
到平面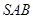 的距离是
的距离是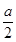 . 其中正确结论的序号是 ______
. 其中正确结论的序号是 ______