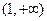题目内容
(本小题满分14分)
已知函数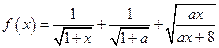 ,
,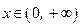 .
.
(1)当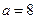 时,求
时,求 的单调区间;
的单调区间;
(2)对任意正数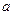 ,证明:
,证明: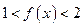 。
。
已知函数
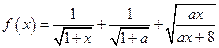 ,
,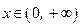 .
.(1)当
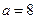 时,求
时,求 的单调区间;
的单调区间;(2)对任意正数
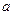 ,证明:
,证明: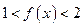 。
。(1)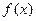 在
在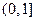 中单调递增,而在
中单调递增,而在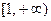 中单调递减。
中单调递减。
(2)证明见解析。
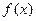 在
在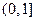 中单调递增,而在
中单调递增,而在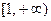 中单调递减。
中单调递减。(2)证明见解析。
(1)当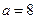 时,
时,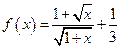 ,求得
,求得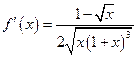 ,
,
于是当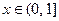 时,
时,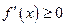 ;而当
;而当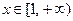 时,
时,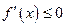 。
。
即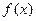 在
在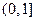 中单调递增,而在
中单调递增,而在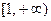 中单调递减。
中单调递减。
(2).对任意给定的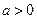 ,
,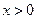 ,由
,由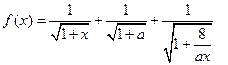 ,
,
若令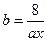 ,则
,则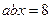 … ① ,而
… ① ,而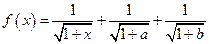 … ②
… ②
(一)、先证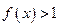 ;因为
;因为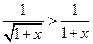 ,
,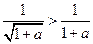 ,
,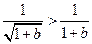 ,
,
又由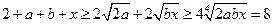 ,得
,得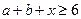 .
.
所以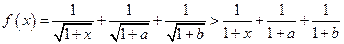
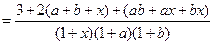
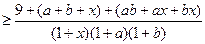
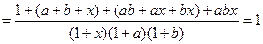 .
.
(二)、再证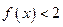 ;由①、②式中关于
;由①、②式中关于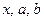 的对称性,不妨设
的对称性,不妨设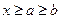 .则
.则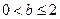
(ⅰ)、当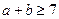 ,则
,则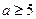 ,所以
,所以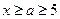 ,因为
,因为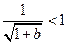 ,
,
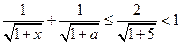 ,此时
,此时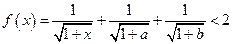 .
.
(ⅱ)、当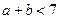 …③,由①得 ,
…③,由①得 ,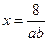 ,
,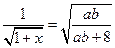 ,
,
因为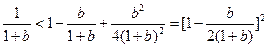 所以
所以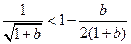 … ④
… ④
同理得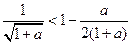 … ⑤ ,于是
… ⑤ ,于是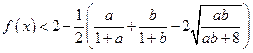 … ⑥
… ⑥
今证明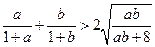 … ⑦, 因为
… ⑦, 因为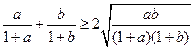 ,
,
只要证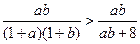 ,即
,即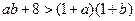 ,也即
,也即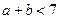 ,据③,此为显然.
,据③,此为显然.
因此⑦得证.故由⑥得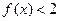 .
.
综上所述,对任何正数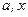 ,皆有
,皆有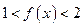 .
.
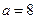 时,
时,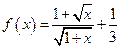 ,求得
,求得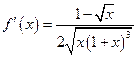 ,
,于是当
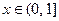 时,
时,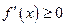 ;而当
;而当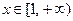 时,
时,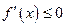 。
。即
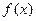 在
在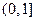 中单调递增,而在
中单调递增,而在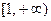 中单调递减。
中单调递减。(2).对任意给定的
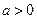 ,
,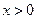 ,由
,由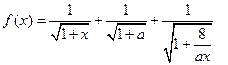 ,
,若令
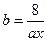 ,则
,则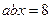 … ① ,而
… ① ,而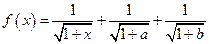 … ②
… ②(一)、先证
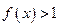 ;因为
;因为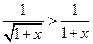 ,
,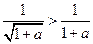 ,
,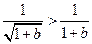 ,
,又由
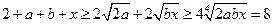 ,得
,得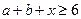 .
.所以
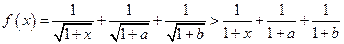
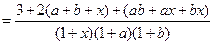
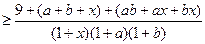
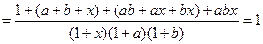 .
.(二)、再证
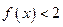 ;由①、②式中关于
;由①、②式中关于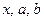 的对称性,不妨设
的对称性,不妨设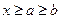 .则
.则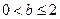
(ⅰ)、当
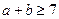 ,则
,则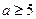 ,所以
,所以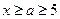 ,因为
,因为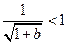 ,
,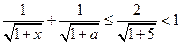 ,此时
,此时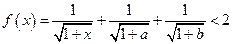 .
.(ⅱ)、当
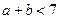 …③,由①得 ,
…③,由①得 ,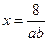 ,
,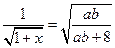 ,
,因为
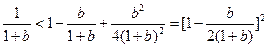 所以
所以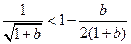 … ④
… ④同理得
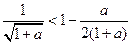 … ⑤ ,于是
… ⑤ ,于是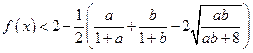 … ⑥
… ⑥今证明
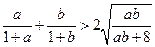 … ⑦, 因为
… ⑦, 因为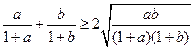 ,
,只要证
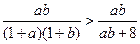 ,即
,即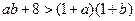 ,也即
,也即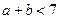 ,据③,此为显然.
,据③,此为显然.因此⑦得证.故由⑥得
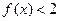 .
.综上所述,对任何正数
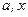 ,皆有
,皆有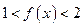 .
.
练习册系列答案
相关题目
 ,
, 记
记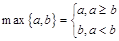 ,函数
,函数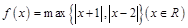 的最小值是 .
的最小值是 . 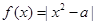 在区间[-1,1]上的最大值
在区间[-1,1]上的最大值 的最小值是 ( )
的最小值是 ( )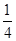

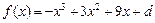 。
。 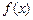 的单调区间;
的单调区间; 上的最小值为
上的最小值为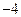 ,求实数
,求实数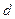 以及在该区间上的最大值.
以及在该区间上的最大值.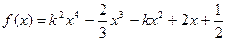 在(1,2)上递减,在(2,-∞)上递增.
在(1,2)上递减,在(2,-∞)上递增. ,满足
,满足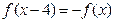 ,且在区间[0,2]上是增函数,则( ).
,且在区间[0,2]上是增函数,则( ). 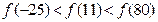
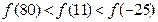
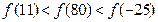
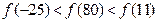
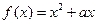 ,
,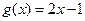 ,
,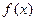 的图像恒在直线
的图像恒在直线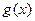 的上方,试求
的上方,试求 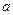 的取值集合;
的取值集合;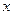 的不等式:
的不等式: 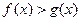 。
。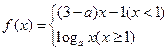 是
是 上的增函数,那么
上的增函数,那么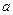 的取值范围是
的取值范围是