题目内容
(本小题满分12分)
已知过点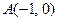 的动直线
的动直线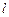 与圆
与圆 :
: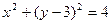 相交于
相交于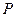 、
、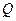 两点,
两点,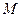 是
是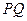 中点,
中点, 与直线
与直线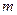 :
: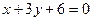 相交于
相交于 .
.
(1)求证:当 与
与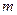 垂直时,
垂直时, 必过圆心
必过圆心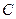 ;
;
(2)当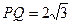 时,求直线
时,求直线 的方程;
的方程;
(3)探索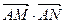 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.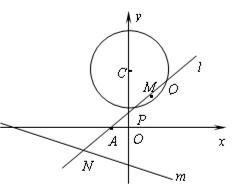
已知过点
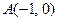 的动直线
的动直线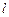 与圆
与圆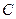 :
: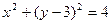 相交于
相交于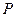 、
、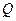 两点,
两点,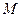 是
是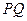 中点,
中点, 与直线
与直线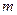 :
: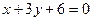 相交于
相交于 .
.(1)求证:当
 与
与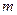 垂直时,
垂直时, 必过圆心
必过圆心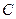 ;
;(2)当
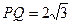 时,求直线
时,求直线 的方程;
的方程;(3)探索
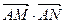 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
(1)略
(2)直线 的方程为
的方程为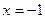 或
或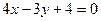
(3)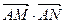 与直线
与直线 的斜率无关,且
的斜率无关,且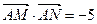 .
.
(2)直线
 的方程为
的方程为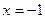 或
或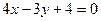
(3)
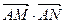 与直线
与直线 的斜率无关,且
的斜率无关,且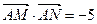 .
.(1)∵ 与
与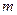 垂直,且
垂直,且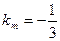 ,
,
∴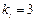 ,故直线
,故直线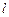 方程为
方程为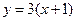 ,
,
即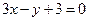 …………………… …2分
…………………… …2分
∵圆心坐标(0,3)满足直线 方程,
方程,
∴当 与
与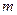 垂直时,
垂直时, 必过圆心
必过圆心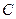 -----------------…3分
-----------------…3分
(2)①当直线 与
与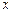 轴垂直时, 易知
轴垂直时, 易知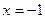 符合题意…………………4分
符合题意…………………4分
②当直线 与
与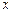 轴不垂直时,∵
轴不垂直时,∵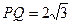 ,∴
,∴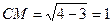 ,
,
则由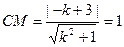 ,得
,得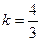 , ∴直线
, ∴直线 :
: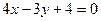 .
.
故直线 的方程为
的方程为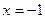 或
或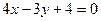 --------------------------------6分
--------------------------------6分
(3)∵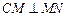 ,
,
∴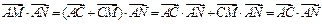 ------------8分
------------8分
①当 与
与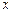 轴垂直时,易得
轴垂直时,易得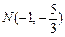 ,则
,则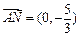 ,又
,又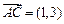 ,
,
∴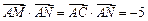 ---------------------------------------------------10分
---------------------------------------------------10分
当 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为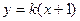 ,
,
则由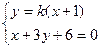 ,
,
得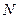 (
(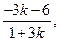
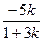 ),则
),则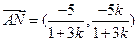
∴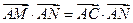 =
=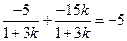
综上所述,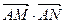 与直线
与直线 的斜率无关,且
的斜率无关,且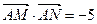 .-------------12分
.-------------12分
 与
与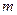 垂直,且
垂直,且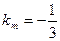 ,
,∴
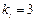 ,故直线
,故直线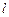 方程为
方程为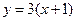 ,
,即
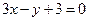 …………………… …2分
…………………… …2分∵圆心坐标(0,3)满足直线
 方程,
方程,∴当
 与
与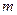 垂直时,
垂直时, 必过圆心
必过圆心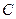 -----------------…3分
-----------------…3分(2)①当直线
 与
与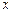 轴垂直时, 易知
轴垂直时, 易知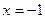 符合题意…………………4分
符合题意…………………4分②当直线
 与
与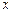 轴不垂直时,∵
轴不垂直时,∵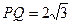 ,∴
,∴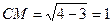 ,
, 则由
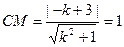 ,得
,得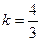 , ∴直线
, ∴直线 :
: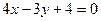 .
. 故直线
 的方程为
的方程为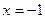 或
或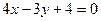 --------------------------------6分
--------------------------------6分(3)∵
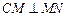 ,
,∴
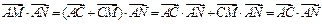 ------------8分
------------8分①当
 与
与 轴垂直时,易得
轴垂直时,易得 ,则
,则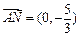 ,又
,又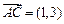 ,
,∴
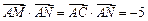 ---------------------------------------------------10分
---------------------------------------------------10分当
 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为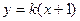 ,
,则由
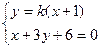 ,
,得
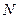 (
(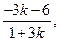
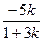 ),则
),则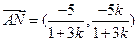
∴
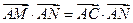 =
=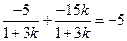
综上所述,
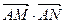 与直线
与直线 的斜率无关,且
的斜率无关,且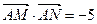 .-------------12分
.-------------12分
练习册系列答案
相关题目
 过定点
过定点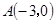 ,并且在定圆
,并且在定圆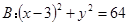 的内部与其相内切,求动圆圆心
的内部与其相内切,求动圆圆心



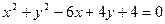 .
.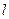 过点P且与圆心C的距离为1,求直线
过点P且与圆心C的距离为1,求直线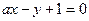 与圆C交于A、B两点,是否存在实数
与圆C交于A、B两点,是否存在实数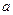 ,使得过点P(2,0)的直线
,使得过点P(2,0)的直线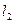 垂直平
垂直平 过点
过点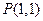 且与圆M:
且与圆M: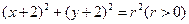 关于直线
关于直线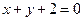 对称
对称 作两条相异直线分别与圆
作两条相异直线分别与圆 、
、
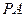 与直线
与直线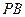 互相垂直,求
互相垂直,求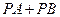 的最大值;
的最大值;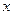 轴分别交于
轴分别交于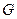 、
、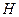 ,且
,且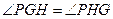 ,
,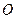 为坐标原点,试判断直线
为坐标原点,试判断直线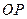 与
与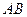 是否平行?请说明理由.
是否平行?请说明理由.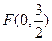 ,动圆P经过点F且和直线
,动圆P经过点F且和直线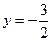 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W.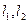 分别交曲线W与A、B和C、D,求四边形ACBD面积的最小值。
分别交曲线W与A、B和C、D,求四边形ACBD面积的最小值。 与圆
与圆 的公共弦长为
的公共弦长为 ,a=_______
,a=_______ ,
, 满足
满足 ,那么
,那么 的取值范围是
的取值范围是  和圆:
和圆: 交于
交于 两点,
两点, 的垂直平分线的方程是( )
的垂直平分线的方程是( )



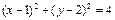 关于直线
关于直线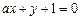 的对称圆为
的对称圆为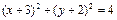 ,
, ____________.
____________.