题目内容
设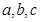
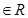 ,则“2b=a+c”是“a,b,c三个数成等差数列”的
,则“2b=a+c”是“a,b,c三个数成等差数列”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
C
解析试题分析:若a+c=2b则有c-b=b-a所以a、b、c成等差数列;
反之,若a、b、c成等差数列则有a+c=2b;
所以a+c=2b是a、b、c成等差数列的充要条件.
故选C.
考点:本题主要考查了判断一个命题是另一个命题的什么条件,应该先确定好条件,然后两边互推,利用充要条件的有关定义进行判断即可.
点评:解决该试题的关键是利用等差数列的定义判断前者能推出后者;反之,也成立.利用充要条件的定义得到结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题中,真命题是.
A.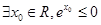 | B.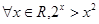 |
C.a+b=0的充要条件是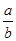 =-1 =-1 | D.a>1,b>1是ab>1的充分条件 |
“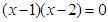 ”是“
”是“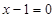 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“AB>0”是“方程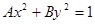 表示椭圆”的 ( )
表示椭圆”的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题:“若x2<1,则-1 ≤ x<1”的逆否命题是
| A.若x2≥1,则x<-1,或x≥1 | B.若-1≤x<1,则x2<1 |
| C.若x≤-1,或x>1,则x2≥1 | D.若x<-1,或x≥1,则x2≥1 |
若m∈R,则“m=1”是“∣m∣=1”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“存在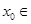 R,
R,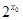
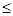 0”的否定是( )
0”的否定是( )
A.不存在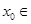 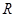 , ,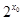 >0 >0 | B.存在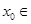 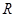 , , 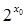 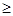 0 0 |
C.对任意的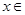 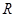 , , 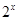 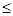 0 0 | D.对任意的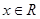 , ,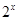 >0 >0 |