题目内容
命题:“若x2<1,则-1 ≤ x<1”的逆否命题是
| A.若x2≥1,则x<-1,或x≥1 | B.若-1≤x<1,则x2<1 |
| C.若x≤-1,或x>1,则x2≥1 | D.若x<-1,或x≥1,则x2≥1 |
D
解析试题分析:先否定原命题的题设做结论,就得到原命题的逆否命题.
∵“x2<1”的否定为“x2≥1”.“-1≤x<1”的否定是“x<-1或x≥1”.
∴命题“若x2<1,则-1≤x<1”的逆否命题是:“若x≥1或x<-1,则x2≥1”.
故答案选D.
考点:本题主要考查了四种命题的表示和求解。
点评:解决该试题的关键是四种命题的相互转化,解题时要认真审题,注意.“-1 ≤ x<1”的否定是“x<-1或x≥1”.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
已知命题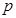 :
: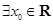 ,
,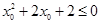 ,那么下列结论正确的是 ( )
,那么下列结论正确的是 ( )
A.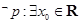 , ,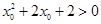 | B.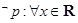 , ,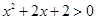 |
C.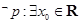 , ,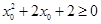 | D.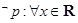 , ,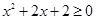 |
下面四个条件中,使 成立的充分而不必要的条件是
成立的充分而不必要的条件是
A. | B. | C. | D.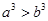 |
若命题 ;命题
;命题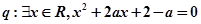
若命题“ ”是真命题,则实数
”是真命题,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
设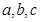
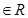 ,则“2b=a+c”是“a,b,c三个数成等差数列”的
,则“2b=a+c”是“a,b,c三个数成等差数列”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列全称命题中假命题的个数是()
①2x+1是整数(x∈R)②对所有的x∈R ,x>3③对任意一个x∈z,2x2+1为奇数
| A.0 | B.1 | C.2 | D.3 |
已知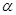 ,
,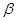 表示两个不同的平面,
表示两个不同的平面,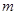 为平面
为平面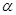 内的一条直线,则“
内的一条直线,则“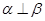 ”是“
”是“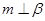 ”的( )
”的( )
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
命题p:3是奇数,q:5是偶数,则下列说法中正确的是( ).
| A.p或q为真 | B.p且q为真 |
| C.非p为真 | D.非q为假 |
“ ”是“方程
”是“方程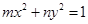 表示焦点在y轴上的椭圆”的( )
表示焦点在y轴上的椭圆”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |