题目内容
【题目】在平面直角坐标系中,点![]() 为曲线
为曲线![]() 上任意一点,且
上任意一点,且![]() 到定点
到定点![]() 的距离比到
的距离比到![]() 轴的距离多1.
轴的距离多1.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 分别作倾斜角互补的直线
分别作倾斜角互补的直线![]() ,
, ![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
, ![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,若
两点,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)利用![]() 到定点的距离和到定直线的距离的关系,列出方程即为曲线
到定点的距离和到定直线的距离的关系,列出方程即为曲线![]() 方程;(2)先考虑特殊情况,当
方程;(2)先考虑特殊情况,当![]() 的横坐标小于零时,求得其纵坐标为
的横坐标小于零时,求得其纵坐标为![]() 不合题意.当
不合题意.当![]() 的横坐标不小于零时,曲线的方程可化为
的横坐标不小于零时,曲线的方程可化为![]() ,分别设出
,分别设出![]() 的坐标,求出斜率
的坐标,求出斜率![]() 利用两个斜率相等,可求得直线
利用两个斜率相等,可求得直线![]() 的方程,利用抛物线的弦长公式可求得
的方程,利用抛物线的弦长公式可求得![]() 的纵坐标.
的纵坐标.
试题解析:(1)设![]() ,则
,则![]() ,此即为
,此即为![]() 的方程,
的方程,
(2)当![]() 的横坐标小于零时,
的横坐标小于零时, ![]() ,即
,即![]() ,不合题意,
,不合题意,
当![]() 的横坐标不小于零时,
的横坐标不小于零时, ![]() ,设
,设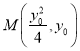 ,
, 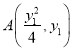 ,
, 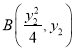 则
则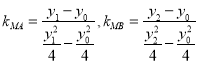 .
.
![]() 直线
直线![]() 的倾斜角互补,
的倾斜角互补, ![]() 即
即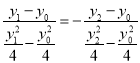 ,化简得
,化简得![]() ,
,
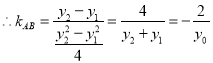 .
.
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,代入
,代入![]() 得,
得, ![]() ,
,
![]() 又
又![]() ,即
,即![]() ,解得
,解得![]()
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
【题目】某中学开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下图是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
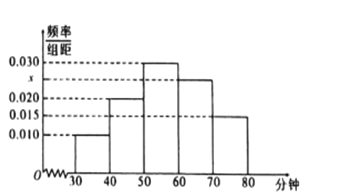
(Ⅰ) 求![]() 的值并估计全校3000名学生中“读书迷”大概有多少?(将频率视为概率)
的值并估计全校3000名学生中“读书迷”大概有多少?(将频率视为概率)
(Ⅱ)根据已知条件完成下面![]() 的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
的列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
附: 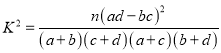 ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |