Question

【题目】已知（为常数）.

（1）求的极值；

（2）设，记，已知为函数是两个零点，求证： .

Answer 1

【答案】（1）的极大值为，无极小值;（2）见解析.

【解析】试题分析：(1) 求导，判断单调性得极值即可.

(2) 先在上构造函数和比较大小，再在上利用函数单调性得.

试题解析：（1）,由得，

且时， ， 时， .

故函数的单调递增区间为，单调递减区间为.

所以，函数的极大值为，无极小值.

（2）由及（1）知的单调递增区间为，单调递减区间为.

由条件知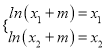，即,

构造函数,知与图像两交点的横坐标为， ,

，由得，易知函数的单调递减区间为，单调递减区间为.

欲证，只需证，不妨设，

考虑到在上递增，只需证,

由知，只需证,

令，

则，

即单调增，注意到，

结合知，即成立，

即成立.

点睛:本题考查的是函数的极值问题和极值点偏移问题.求极值时要注意判断在导数为的点两侧的符号，异号时为极值点，要记得判断是极大值还是极小值 ，否则不是极值点;在第二问极值点偏移中，要解决两个问题，一是在上构造函数和比较大小，二是在上利用函数单调性.