题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程;
)处的切线方程;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)已知![]() ,对于函数
,对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,其中
,其中![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记
,记![]() ,若
,若![]() 求证
求证![]()
【答案】(Ⅰ) ![]() ;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
;(Ⅱ)答案见解析;(Ⅲ)证明见解析.
【解析】【试题分析】(Ⅰ)由题设条件先求出函数![]() 导数,再借助导数的几何意义求出切线的斜率
导数,再借助导数的几何意义求出切线的斜率![]() ;(Ⅱ)先求函数
;(Ⅱ)先求函数![]() 的导数
的导数![]() 再依据实数
再依据实数![]() 的取值范围进行分类求出其单调区间;(Ⅲ)分别求出k=
的取值范围进行分类求出其单调区间;(Ⅲ)分别求出k=![]()
![]() 和
和![]() 将问题转化为证明
将问题转化为证明![]() ,然后设
,然后设![]() 再构造函数
再构造函数![]() ,最后借助导数知识推断函数
,最后借助导数知识推断函数![]() 在
在![]() 内单调递减,进而推得
内单调递减,进而推得![]() 从而证得
从而证得![]() :
:
解析:(Ⅰ)当![]() 时,
时, ![]()
![]()
![]()
又![]()
![]() 函数
函数![]() 的图象在点(1,
的图象在点(1, ![]() )处的切线方程为:
)处的切线方程为: ![]() ,
,
即![]()
(Ⅱ) ![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在定义域内单调递增;
在定义域内单调递增;
当![]() 时,令
时,令![]() 解得,
解得, ![]()
![]()
则 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
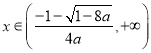 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
综上, ![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ;
;
![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为 ,
,
![]() 的单调递增区间为
的单调递增区间为
(Ⅲ)证明: ![]()
![]()
![]()
![]() ,
,
又![]() ,
, ![]()
![]()
![]()
要证: ![]() ,只需证
,只需证![]()
即证: ![]() ,设
,设![]()
令![]() 则
则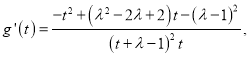
令![]()
对称轴![]() .
.
![]()
![]() ,故
,故![]() 在
在![]() 内单调递减,则
内单调递减,则![]() ;
;
故![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

