题目内容
1.若实数x,y满足x≥y>0,且$x=4\sqrt{y}+2\sqrt{x-y}$,则x的取值范围是(4,20].分析 设$\sqrt{y}$=t则可知t>0,重新整理等式,利用一元二次方程根的情况,要使方程有正数根,需要△≥0且f(0)>0,解不等式组即可求得x的范围
解答 解:设$\sqrt{y}$=t,t>0,
则$\sqrt{x-y}$=$\sqrt{x-{t}^{2}}$,
∴x=4t+2$\sqrt{x-{t}^{2}}$,
整理得20t2-8xt+x2-4x=0,
要使方程有正数解需$\left\{\begin{array}{l}{△=64{x}^{2}-80({x}^{2}-4x)≥0}\\{f(0)={x}^{2}-4x>0}\end{array}\right.$,
求得4<x≤20,
故答案为:(4,20]
点评 本题主要考查了函数和方程思想的运用.这道题需要运用转化和化归的思想,把问题转化为函数和方程的问题,利用根的分布来解决x的范围问题.

练习册系列答案
相关题目
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
13.某正三棱柱的三视图如图所示,其中正(主)视图是正方形,该正三棱柱的侧视图的面积是( )
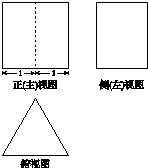

| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
9.为了得到函数y=3cos2x的图象,只需把函数$y=3sin(2x+\frac{π}{6})$的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
16.已知a,b∈R,则“ab=4”是“直线2x+ay-1=0与bx+2y+1=0平行”的( )
| A. | 充分必要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
13.a的值由如图程序框图算出,则二项式($\sqrt{x}$-$\frac{a}{x}$)9展开式的常数项为( )


| A. | T4=53×${C}_{9}^{3}$ | B. | T6=-55×${C}_{9}^{5}$ | C. | T5=74×${C}_{9}^{4}$ | D. | T4=-73×${C}_{9}^{3}$ |