题目内容
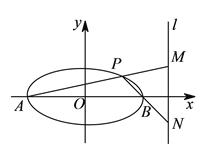
【题目】已知椭圆![]() (
(![]() 是大于
是大于![]() 的常数)的左、右顶点分别为
的常数)的左、右顶点分别为![]() 、
、![]() ,点
,点![]() 是椭圆上位于
是椭圆上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() 、
、![]() 与直线
与直线![]() 分别交于
分别交于![]() 、
、![]() 两点(设直线
两点(设直线![]() 的斜率为正数).
的斜率为正数).
(Ⅰ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,求证
,求证![]() 为定值.
为定值.
(Ⅱ)求线段![]() 的长度的最小值.
的长度的最小值.
(Ⅲ)判断“![]() ”是“存在点
”是“存在点![]() ,使得
,使得![]() 是等边三角形”的什么条件?(直接写出结果)
是等边三角形”的什么条件?(直接写出结果)
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)既不充分也不必要条件.
;(Ⅲ)既不充分也不必要条件.
【解析】试题分析:
(Ⅰ)由题意可得直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,据此计算则有
,据此计算则有![]() 为定值
为定值![]() .
.
(Ⅱ)结合点的坐标求得MN的长度表达式,结合均值不等式的结论可得线段![]() 长度的最小值为
长度的最小值为![]() .
.
(Ⅲ)结合圆锥曲线的性质可知“![]() ”是“存在点
”是“存在点![]() ,使得
,使得![]() 是等边三角形”的既不充分也不必要条件.
是等边三角形”的既不充分也不必要条件.
试题解析:
(Ⅰ)设![]() ,则
,则![]() ,即
,即![]() ,
,
∴直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
∴![]() ,
,
故![]() 为定值
为定值![]() .
.
(Ⅱ)直线![]() 方程为
方程为![]() ,∴
,∴![]() 点坐标
点坐标![]() ,
,
直线![]() 方程为
方程为![]() ,∴
,∴![]() 点坐标
点坐标![]() ,
,
∴![]() ,
,
∴![]()
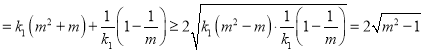 .
.
故线段![]() 长度的最小值为
长度的最小值为![]() .
.
(Ⅲ)“![]() ”是“存在点
”是“存在点![]() ,使得
,使得![]() 是等边三角形”的既不充分也不必要条件.
是等边三角形”的既不充分也不必要条件.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目