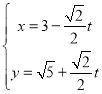题目内容
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;

(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
【答案】(1)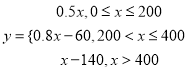 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:1)根据电价的分档情况,可以写出分段函数,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ;(2)由(1)可知:当
;(2)由(1)可知:当![]() 时,
时, ![]() ,则
,则![]() ,根据频率分布直方图可知
,根据频率分布直方图可知![]() ,解出
,解出![]() ;(3)分别求出各组中值点的电价,并求其概率(频率),再求平均值
;(3)分别求出各组中值点的电价,并求其概率(频率),再求平均值![]() .
.
试题解析:
(1)当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 与
与![]() 之间的函数解析式为:
之间的函数解析式为: 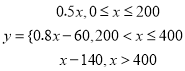 ;
;
(2)由(1)可知:当![]() 时,
时, ![]() ,则
,则![]() ,
,
结合频率分布直方图可知: ![]() ,
,
∴![]() ;
;
(3)由题意可知![]() 可取50,150,250,350,450,550.
可取50,150,250,350,450,550.
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
故![]() 的概率分布列为:
的概率分布列为:
| 25 | 75 | 140 | 220 | 310 | 410 |
| 0.1 | 0.2 | 0.3 | 0.2 | 0.15 | 0.05 |
所以随机变量![]() 的数学期望
的数学期望
![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.