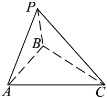
题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 为定点,点
为定点,点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() ,且
,且![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为曲线
为曲线![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.问
两点.问![]() 是否为定值?若是,求
是否为定值?若是,求![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
【答案】(1)![]() ;(2)是定值,
;(2)是定值,![]() .
.
【解析】
(1)设出M的坐标为![]() ,采用直接法求曲线
,采用直接法求曲线![]() 的方程;
的方程;
(2)设AB的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,求出AT方程,联立直线
,求出AT方程,联立直线![]() 方程得D点的坐标,同理可得E点的坐标,最后利用向量数量积算
方程得D点的坐标,同理可得E点的坐标,最后利用向量数量积算![]()
![]() 即可.
即可.
(1)设动点M的坐标为![]() ,由
,由![]() 知
知![]() ∥
∥![]() ,又
,又![]() 在直线
在直线![]() 上,
上,
所以P点坐标为![]() ,又
,又![]() ,点
,点![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() ,
,![]() ,
,
由![]() 得
得![]() ,即
,即![]() ;
;
(2)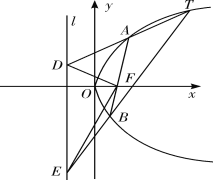
设直线AB的方程为![]() ,代入
,代入![]() 得
得![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,
,![]() ,设
,设![]() ,则
,则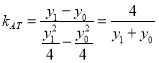 ,
,
所以AT的直线方程为![]() 即
即![]() ,令
,令![]() ,则
,则
![]() ,所以D点的坐标为
,所以D点的坐标为![]() ,同理E点的坐标为
,同理E点的坐标为![]() ,于是
,于是![]()
![]() ,
,
![]()
![]() ,所以
,所以![]()
![]()
![]()
![]()
![]()
![]()
![]() ,从而
,从而![]()
![]() ,
,
所以![]() 是定值.
是定值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和![]() 列联表:
列联表:
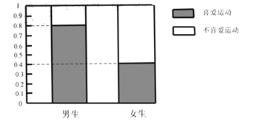
喜爱运动 | 不喜爱运动 | 总计 | |
男生 |
|
| 30 |
女生 |
|
| 20 |
总计 | 50 |
(1)求出列联表中![]()
![]()
![]()
![]() 的值;
的值;
(2)是否有![]() 的把握认为喜爱运动与性别有关?附:参考公式和数据:
的把握认为喜爱运动与性别有关?附:参考公式和数据: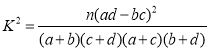 ,(其中
,(其中![]() )
)
0.500 | 0.100 | 0.050 | 0.010 | 0.001 | |
| 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |