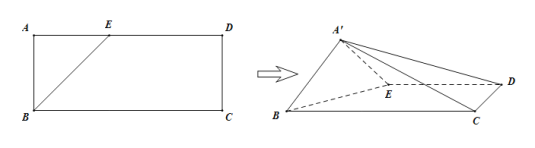
题目内容
【题目】如图,三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
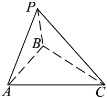
(1)求证:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .根据
.根据![]() ,得
,得 ![]() ,再由
,再由![]() ,根据线面垂直的判定定理得
,根据线面垂直的判定定理得![]() 平面
平面![]() ,则
,则![]() ,再利用三线合一证明.
,再利用三线合一证明.
(2)由![]() 三条直线两两垂直,建立空间直角坐标系,分别求得平面
三条直线两两垂直,建立空间直角坐标系,分别求得平面![]() 和平面
和平面![]() 的一个法向量,再利用二面角的向量法公式求解.
的一个法向量,再利用二面角的向量法公式求解.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
又![]() OC
OC![]() 平面
平面![]() ,
,![]()
![]() ,
,
而![]() 是
是![]() 的中点,
的中点,![]()
![]() .
.
(2)![]() 平面
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
再由(1)可知![]() 三条直线两两垂直.
三条直线两两垂直.
以![]() 所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
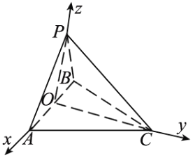
由条件可得![]() ,
,![]() .
.
则![]() ,
,
![]()
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由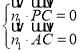 可得
可得
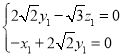 ,
,
令![]() ,则
,则![]() .
.
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() .
.
由图易知,二面角![]() 为锐角,
为锐角,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】棉花的优质率是以其纤维长度来街量的,纤维越长的棉花晶质越高.棉花的品质分类标准为:纤维长度小于等于![]() 的为粗绒棉,纤维长度在
的为粗绒棉,纤维长度在![]() 的为细绒棉,纤维长度大于
的为细绒棉,纤维长度大于![]() 的为长绒棉,其中纤维长度在
的为长绒棉,其中纤维长度在![]() 以上的棉花又名“军海1号”.某采购商从新疆某一棉花基地抽测了
以上的棉花又名“军海1号”.某采购商从新疆某一棉花基地抽测了![]() 根棉花的纤维长度,得到数据如下图频率分布表所示:
根棉花的纤维长度,得到数据如下图频率分布表所示:
纤维长度 |
|
|
|
|
根数 |
|
|
|
|
(1)若将频率作为概率, 根据以上数据,能否认为该基地的这批棉花符合“长绒棉占全部棉花的![]() 以上”的要求?
以上”的要求?
(2)用样本估计总体, 若这批榨花共有![]() ,基地提出了两种销售方案给采购商参考.方案一:不分等级卖出,每千克按
,基地提出了两种销售方案给采购商参考.方案一:不分等级卖出,每千克按![]() 元计算,方案二:对
元计算,方案二:对![]() 棉花先分等级再销售,分级后不同等级的棉花售价如下表:
棉花先分等级再销售,分级后不同等级的棉花售价如下表:
纤维长度 |
|
|
|
|
售价 |
|
|
|
|
从来购商的角度,请你帮他决策一下该用哪个方案.
(3)用分层抽样的方法从长绒棉中抽取6根棉花,再从此![]() 根棉花中抽取两根进行检验.求抽到的两根棉花只有一根是“军海1号”的概率.
根棉花中抽取两根进行检验.求抽到的两根棉花只有一根是“军海1号”的概率.